Metric and Topological Spaces
Separation axioms
We saw earlier how the ideas of convergence could be interpreted in a topological rather than a metric space:
A sequence (ai) converges to 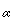 if every open set containing
if every open set containing 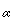 contains all but a finite number of the {ai}.
contains all but a finite number of the {ai}.
Unfortunately, this definition does not give some of thr "nice" properties we get in a metric space.
For example, if a sequence in a metric space converges, it has a unique limit, but in a topological space this need not happen. For example, in R with the trivial topology every sequence converges to every point.
To recove the nice properties of convergence we need to have "enough" open sets in the topology. Topologists have devised various separation axioms to classify how this happens.
Definition
A topological space X is called Hausdorff if every pair of points can be separated by open sets.
That is, if x1 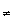 x2
x2  X then there are disjoint open sets U1 and U2 with x1
X then there are disjoint open sets U1 and U2 with x1  U1 and x2
U1 and x2  U2 .
U2 .
Remarks
- Felix Hausdorff (1869 to 1942) introduced this idea. He was also responsible for the first formulation of the idea of fractional dimension encountered in fractal Geometry.
- The Hausdorff condition is sometimes called T2 . This axiom is one of a number of separation axioms: T0 , T1 , T2 , T3 , T31/2 , T4 .
These were named by Heinreich Tietze (1880 to 1964) in 1923. The T stands for trennung (= separation in German). Some references call them the Tychonoff axioms after Andrei Tychonoff (1906 to 1993).
Just for the record, T0 spaces are sometimes called Kolmogorov spaces, T1 spaces are called Fréchet spaces, T2 spaces are Hausdorff, T3 spaces are regular, T31/2 spaces are completely regular. We will see about T4 spaces shortly.
See this link for more details.
- In a Hausdorff space, distinct points are "housed off" from one another by open sets.
Theorem
Every metric space is Hausdorff.
Proof

Theorem
In any Hausdorff space sequences have at most one limit.
Proof

Theorem
In a Hausdorff space every point is a closed set.
Proof

Remark
It follows that every finite set is closed in a Hausdorff space and the topology is therefore stronger than the cofinite topology.
The other separation axiom we will consider is:
Definition
A topological space X is called normal if every disjoint pair of closed sets can be separated by open sets.
That is, if A1 and A2 are disjoint closed subsets of X then there are disjoint open sets U1 and U2 with A1  U1 and A2
U1 and A2  U2 .
U2 .
Remark
If every point is a closed set (that is T1) then such a normal space is Hausdorff. [normal + T1 = T4]
Theorem
Every metric space is normal.
Proof

Remark
Note that the distance between disjoint closed sets may be 0 (but they can still be separated by open sets).
Examples
- As above, all metric spaces are both Hausdorrf and normal.
- The space X = {a, b} with
 = {
= { , X, {a} } is not Hausdorff since a, b cannot be separated by open sets.
, X, {a} } is not Hausdorff since a, b cannot be separated by open sets.
It is, however, normal since there are no non-empty disjoint closed sets.
Remarks
- Finding a Hausdorff space which is not normal is possible, but tricky!
- By demanding more separation axioms one gets closer to a metric space. Paul Urysohn (1898 to 1924) proved in 1923 that any T4 space with a countable basis is metrisable (that is, the topology may be obtained from a metric).
In fact this is not a necessary condition for metrisability. For example, R with the discrete topology is metrisable but does not have a countable basis. Marshall Stone (1903 to 1989) and R H Bing (1914 to 1986) found a necessary and sufficient condition for metrisability in 1950.
JOC February 2004
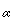 if every open set containing
if every open set containing 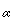 contains all but a finite number of the {ai}.
contains all but a finite number of the {ai}.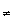 x2
x2  X then there are disjoint open sets U1 and U2 with x1
X then there are disjoint open sets U1 and U2 with x1 
 U1 and A2
U1 and A2  = {
= { , X, {a} } is not Hausdorff since a, b cannot be separated by open sets.
, X, {a} } is not Hausdorff since a, b cannot be separated by open sets.