Metric and Topological Spaces
More identification spaces
A sphere (again)
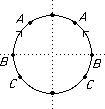 Start with a disc. Use an equivalence relation to identify points on the boundary as shown.
Start with a disc. Use an equivalence relation to identify points on the boundary as shown.
That is, (x1 , y1) ~ (x2 , y2) if (x1 , y1) = (x2 , y2) or
x1 = -x2 and y1 = y2 and x12 + y12 = 1 and x22 + y22 = 1.
This is like folding a piece of pastry to make a "bridie" or "pastie"
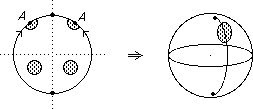 A inverse image of a neighbourhood of a point in X/~ is like an ordinary neighbourhood for an interior point and is the union of a pair of "semi-discs" for a point on the boundary.
A inverse image of a neighbourhood of a point in X/~ is like an ordinary neighbourhood for an interior point and is the union of a pair of "semi-discs" for a point on the boundary.
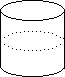
A cylinder
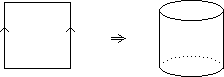 Glue the ends of a strip using the same equivalence relation used to make the circle from a closed interval.
Glue the ends of a strip using the same equivalence relation used to make the circle from a closed interval.
This space then gets the same topology as a subset of R3 , as a product S1  I and as an identification space.
I and as an identification space.
A Möbius band
This was invented by the German mathematician August Möbius (1790 to 1868) in 1858.
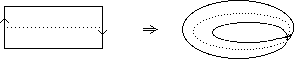 "Glue" a strip as above, but this time after a half twist.
"Glue" a strip as above, but this time after a half twist.
Note that the "centre line" becomes a circle in R3.
Remark
 One can make a cylinder by giving the strip a full twist before gluing. This produces something homeomorphic to the above cylinder but with an embedding in R3 in a very different way. You can see this by cutting the surface along the dotted line shown.
One can make a cylinder by giving the strip a full twist before gluing. This produces something homeomorphic to the above cylinder but with an embedding in R3 in a very different way. You can see this by cutting the surface along the dotted line shown.
JOC February 2004
 Start with a disc. Use an equivalence relation to identify points on the boundary as shown.
Start with a disc. Use an equivalence relation to identify points on the boundary as shown.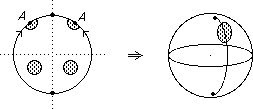 A inverse image of a neighbourhood of a point in X/~ is like an ordinary neighbourhood for an interior point and is the union of a pair of "semi-discs" for a point on the boundary.
A inverse image of a neighbourhood of a point in X/~ is like an ordinary neighbourhood for an interior point and is the union of a pair of "semi-discs" for a point on the boundary.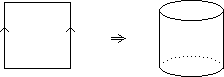 Glue the ends of a strip using the same equivalence relation used to make the circle from a closed interval.
Glue the ends of a strip using the same equivalence relation used to make the circle from a closed interval.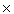 I and as an identification space.
I and as an identification space. "Glue" a strip as above, but this time after a half twist.
"Glue" a strip as above, but this time after a half twist. One can make a cylinder by giving the strip a full twist before gluing. This produces something homeomorphic to the above cylinder but with an embedding in R3 in a very different way. You can see this by cutting the surface along the dotted line shown.
One can make a cylinder by giving the strip a full twist before gluing. This produces something homeomorphic to the above cylinder but with an embedding in R3 in a very different way. You can see this by cutting the surface along the dotted line shown.