Some topological ideas

Before we look at the formal definitions of metric spaces and their generalisations we will consider some naive examples which lie at the base of some topological considerations.
The basic idea behind topology is the concept of a continuous function.

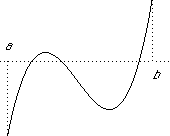
1. For example is the graph of a continuous function on the interval (a, b) of R
   while 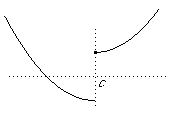is the graph of a function with a discontinuity at c.
   This intuitive concept needs a bit of tinkering to make it rigorous.

2. For maps from R² to R² which are transformations of the plane:
   A continuous map stretches but does not to tear. Think of crumpling up the plane and then flattening it down.
   You could even stretch it (a finite amount). The important thing is that close points are mapped to close points.
   If you "tear" the plane, points which were close together on either side of the tear will be ripped apart and may not end up close: that is a discontinuity.
   We will make all this at rigorous later.

3. If you can stretch one subset A of (say) R³ into another one B, using a continuous map and vice-versa, we will say that A and B are topologically equivalent or (technical term) homeomorphic.
   Again, we will make of this at rigorous later, but here are some examples:
   
   1. 

   2. 

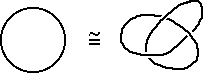   3. in R³.

      But (amazingly) if you removed each of these knots from R³, the sets that are left are not homeomorphic.
      It is things like this last example that spurred it topologists on to classification of things like knots.

   4. The ma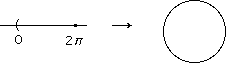p    from the interval (0, 2p] in R to the unit circle in C given by t e^it is a continuous one-one map. It has a well-defined inverse.
      What stops it being a homeomorphism?
      Answer: the inverse map is not continuous at 1.
      "Sticking the things" together means that you would have to tear them apart to define the inverse.