Revision of real analysis

The basic notions of analysis for R (= a complete ordered field) are :

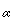
1. A sequence (a_n) in R is convergent to R if:
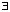   Given > 0 N N such that n > N |a_n - | < .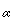

   Informally: thinking of the terms of the sequence as approximations to the limit, the approximation gets better as you go further down the sequence.
   For such a sequence we write (a_n) .

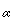2. A function is continuous at p R if:
   Given > 0 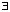> 0 such that |p - x| < |f(p) _ f(x)| < .

   Informally, points close enough to p are mapped close to f(p). By a continuous function we mean one which is continuous at all points where it is defined.

   If you can draw the graph of a function, you should be able to spot whether it is continuous it will not, but functions defined in complicated ways this may be very hard to decide about.