Definition
The sequence (xn) in a metric space is convergent to x
 X if:
X if: | Previous page (Definition and examples of metric spaces) | Contents | Next page (Continuity in metric spaces) |
The definitions given earlier for R generalise very naturally.
Definition
The sequence (xn) in a metric space is convergent to x  X if:
X if:
 > 0
> 0 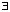 N
N  N such that n > N
N such that n > N  d(xn, x) <
d(xn, x) <  .
. x in the metric space X if the real sequence (d(xn , x))
x in the metric space X if the real sequence (d(xn , x))  0 in R.
0 in R. if a sequence is convergent in one metric, it is convergent in the others.
if a sequence is convergent in one metric, it is convergent in the others.  x and (yi)
x and (yi)  y in R. That is, convergence is componentwise.
y in R. That is, convergence is componentwise.This becomes even more important in:
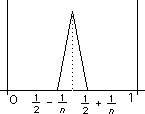
 we have d
we have d (fn , 0) = 1 for all n and so this sequence does not converge to the zero-function in the metric d
(fn , 0) = 1 for all n and so this sequence does not converge to the zero-function in the metric d . In fact it does not converge took any function.
. In fact it does not converge took any function.
We will look at C[0, 1] with the d -metric in more detail later.
-metric in more detail later.
| Previous page (Definition and examples of metric spaces) | Contents | Next page (Continuity in metric spaces) |