A map f between metric spaces is continuous at a point p
 X if
X ifGiven
 > 0
> 0 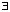
 > 0 such that dX(p, x) <
> 0 such that dX(p, x) < 
 dX(f(p), f(x)) <
dX(f(p), f(x)) <  .
.
| Previous page (Convergence in metric spaces) | Contents | Next page (Neighbourhoods and open sets in metric spaces) |
We look at continuity for maps between metric spaces .
Definition
A map f between metric spaces is continuous at a point p  X if
X if
Given  > 0
> 0 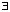
 > 0 such that dX(p, x) <
> 0 such that dX(p, x) < 
 dX(f(p), f(x)) <
dX(f(p), f(x)) <  .
.
Informally: points close to p (in the metric dX) are mapped close to f(p) (in the metric dY).
A continuous function is one which is continuous for all p  X.
X.
Remarks
When one is given a point p and  > 0 the
> 0 the  one needs for the definition may depend on both p and
one needs for the definition may depend on both p and  . It is therefore incorrect to define continuity as:
. It is therefore incorrect to define continuity as:
 p
p  X,
X,  > 0
> 0 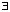
 > 0 such that
> 0 such that  x
x  X with dX(p, x) <
X with dX(p, x) < 
 dX(f(p), f(x)) <
dX(f(p), f(x)) <  .
.
since this would imply that the same choice of  would work for all p.
would work for all p.
As in the prototype R case, one can connect continuity and convergence with:
Theorem
Continuous functions map convergent sequences to convergent sequences.
Formally if f: X  Y is a map between metric spaces which is continuous and (an) is a sequence in X which is
Y is a map between metric spaces which is continuous and (an) is a sequence in X which is
convergent to a point p  X them (f(an)) is a sequence in Y convergent to f(p).
X them (f(an)) is a sequence in Y convergent to f(p).
Proof
Points close to p are mapped close to f(p).
More rigorously: to prove (f(an))  f(p), given
f(p), given  > 0, use continuity at p
> 0, use continuity at p  X to find
X to find  > 0 such that if dX(p, x) <
> 0 such that if dX(p, x) <  then dY(f(p),f(x)) <
then dY(f(p),f(x)) <  .
.
Then use convergence in X to find N  N such that if n > N we have dX(xn,p) <
N such that if n > N we have dX(xn,p) <  . For this N we have dY(f(xn), f(p)) <
. For this N we have dY(f(xn), f(p)) <  and so we have convergence in Y.
and so we have convergence in Y.

In fact, as in the R case, there is a converse to this theorem.
Converse
If all convergent sequences are mapped to convergent sequences then the function is continuous.
More exactly: If (xn)  x
x  (f(xn))
(f(xn))  f(p) then f is continuous at p.
f(p) then f is continuous at p.
Proof
Suppose that f were not continuous at p. Then for some  > 0 we cannot find any choice of
> 0 we cannot find any choice of  to satisfy the continuity condition.
to satisfy the continuity condition.
In particular,  = 1 will not work. Hence for some point x1 we have dX(x1 , p) < 1 but dY(f(x1), f(p))
= 1 will not work. Hence for some point x1 we have dX(x1 , p) < 1 but dY(f(x1), f(p)) 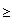
 .
.
Similarly  = 1/2 will not work and so for some point x2 we have dX(x2 , p) < 1/2 but dY(f(x2), f(p))
= 1/2 will not work and so for some point x2 we have dX(x2 , p) < 1/2 but dY(f(x2), f(p)) 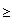
 , ...
, ...
Continue like this to get a sequence (x1 , x2 , x3 , ...) with dX(xn , p) < 1/n but dY(f(xn), f(p)) 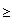
 for each n. But since (xn) has been constructed so that (xn)
for each n. But since (xn) has been constructed so that (xn)  p this contradicts the condition given in the theorem.
p this contradicts the condition given in the theorem.

Remark
Since "nice behaviour on convergent sequences" is a necessary and sufficient condition for continuity, this can be used as the definition of a continuous function.
| Previous page (Convergence in metric spaces) | Contents | Next page (Neighbourhoods and open sets in metric spaces) |