 -neighbourhood of a point p is the set of all points within
-neighbourhood of a point p is the set of all points within  of it.
of it.
| Previous page (Continuity in metric spaces) | Contents | Next page (Limit points and closed sets in metric spaces) |
Although it will not be clear for a little while, the next definition represents the first stage of the generalisation from metric to topological spaces.
An (open)  -neighbourhood of a point p is the set of all points within
-neighbourhood of a point p is the set of all points within  of it.
of it.
Definition
An open neighbourhood of a point p in a metric space (X, d) is the set V (p) = {x
(p) = {x  X | d(x, p) <
X | d(x, p) <  }
}
Examples
 , p +
, p +  ).
).
 one can recognise an
one can recognise an  -neighbourhood of a point (or function) f as the set of functions whose graphs lie in an
-neighbourhood of a point (or function) f as the set of functions whose graphs lie in an  -band around the graph of f.
-band around the graph of f. x in a metric space if every
x in a metric space if every  -neighbourhood contains all but a finite number of terms of (xi).
-neighbourhood contains all but a finite number of terms of (xi). X if every
X if every  -neighbourhood of f(p) contains the image of some
-neighbourhood of f(p) contains the image of some  -neighbourhood of p.
-neighbourhood of p.
We can now use the concept of an  -neighbourhood to define one of the most important ideas in a metric space.
-neighbourhood to define one of the most important ideas in a metric space.
Definition
A subset A of a metric space X is called open in X if every point of A has an  -neighbourhood which lies completely in A.
-neighbourhood which lies completely in A.
Examples

 < min {a, 1-a}. Then V
< min {a, 1-a}. Then V (a)
(a)  (0, 1).
(0, 1).
 (2, 3) is an open set.
(2, 3) is an open set.
 R2 | x2 + y2 < 1} is an open subset of R2 with its usual metric.
R2 | x2 + y2 < 1} is an open subset of R2 with its usual metric. (0, 1)
(0, 1)  (0, 1) ].
(0, 1) ].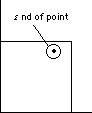
 R2 | f(x, y) < 1} with f(x, y) a continuous function, is an open set.
R2 | f(x, y) < 1} with f(x, y) a continuous function, is an open set.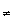 y) every subset is open.
y) every subset is open.
 Ai = A. Then s
Ai = A. Then s  Ai for some i. Since this is open, x has an
Ai for some i. Since this is open, x has an  -neighbourhood lying completely inside Ai and this is also inside A.
-neighbourhood lying completely inside Ai and this is also inside A.
 A
A  B.
B. A and so has an
A and so has an  1-neighbourhood lying in A. Similarly x has an
1-neighbourhood lying in A. Similarly x has an  2-neighbourhood lying in B. So if
2-neighbourhood lying in B. So if  = min {
= min { 1 ,
1 ,  2} this
2} this  -neighbourhood lies in both A and B and hence in A
-neighbourhood lies in both A and B and hence in A  B.
B.
 1 ,
1 ,  2 ,
2 ,  3 , ...} > 0.
3 , ...} > 0. (-1/i, 1/i) = {0} which is not open.
(-1/i, 1/i) = {0} which is not open.
We can now connect the concept of continuity with open sets.
 Y is a continuous function between metric spaces and B
Y is a continuous function between metric spaces and B  Y is open, then f -1(B) is an open subset of X.
Y is open, then f -1(B) is an open subset of X.
Proof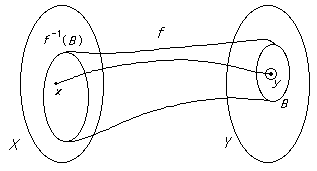
Note that even if f is not a one-one-correspondance (and does not have an inverse function f -1) the set f -1(B) ={x  X | f(x)
X | f(x)  B} still exists.
B} still exists.
Take x  f -1(B). Then f(x) = y
f -1(B). Then f(x) = y  B.
B.
Since B is open the point y has an  -neighbourhood
-neighbourhood  B.
B.
Then, from the definition of continuity this  -neihbourhood contains the image of some
-neihbourhood contains the image of some  -neighbourhood V of x. Since f(V)
-neighbourhood V of x. Since f(V)  B we have V
B we have V  f -1(B) and so x has this
f -1(B) and so x has this  neighbourhood
neighbourhood  f -1(B).
f -1(B).
Hence f -1(B) is open in X.

The converse of this result also holds:
If f:X  Y is a function for which f -1(B) is open in X for every open set B in Y, then f is continuous at every point of X.
Y is a function for which f -1(B) is open in X for every open set B in Y, then f is continuous at every point of X.
Proof
To show that f is continuous at x  X, take B to be an
X, take B to be an  -neighbourhood of y
-neighbourhood of y  Y.
Y.
Then f -1(B) is open in X and so x has a  -neighbourhood in f -1(B). This
-neighbourhood in f -1(B). This  -neighbourhood is mapped inside the
-neighbourhood is mapped inside the  -neighbourhood of f(x) and so f is continuous at x.
-neighbourhood of f(x) and so f is continuous at x.

| Previous page (Continuity in metric spaces) | Contents | Next page (Limit points and closed sets in metric spaces) |