Metric and Topological Spaces
Limit points and closed sets in metric spaces
Definition
If A is a subset of a metric space X then x is a limit point of A if it is the limit of an eventually non-constant sequence (ai) of points of A.
Remarks
- This is the most common version of the definition -- though there are others.
- Limit points are also called accumulation points.
Examples
- R with the usual metric
Sets sometimes contain their limit points and sometimes do not.
- The points 0 and 1 are both limit points of the interval (0, 1).
- The set Z
 R has no limit points.
R has no limit points.
For example, any sequence in Z converging to 0 is eventually constant.
- R2 with the usual metric
The limit points of the open disc {(x, y)  R2 | x2+ y2 < 1} form the closed disc {(x, y)
R2 | x2+ y2 < 1} form the closed disc {(x, y)  R2 | x2+ y2
R2 | x2+ y2 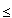 1}.
1}.
Any point on the boundary of the circle is a limit of a sequence of points inside the circle.
- In R every real number is a limit point of the subset Q of rationals.
Proof
Every real number can be approximated arbitrarily closely by a sequence of rationals (by truncating the decimal expansion, say).

Remark
Alternative definitions of a limit point of a subset A are:
- A point x of X is a limit point of A if every
 -nd of x in X meets A in a point
-nd of x in X meets A in a point 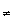 x.
x.
- A point x of X is a limit point of A if every open set of X containing x meets A in a point
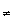 x.
x.
We can connect this idea with the last section by:
Definition
A subset A is said to be a closed subset of X if it contains all its limit points.
Examples
- The subset X is a closed subset of itself. The empty set is closed. Any finite set is closed.
- The closed interval [0, 1] is closed subset of R with its usual metric. There are, however, lots of closed subsets of R which are not closed intervals.
- The closed disc, closed square, etc. are closed subsets of R2.
Then the connection with the last section is:
Theorem
A subset A of a metric space X is closed if and only if its complement X - A is open.
Proof
( ) Suppose A is closed. We need to show that X - A is open. So suppose that x
) Suppose A is closed. We need to show that X - A is open. So suppose that x  X - A. Then some
X - A. Then some  -neighbourhood of x does not meet A (otherwise x would be a limit point of A and hence in A). Thus this
-neighbourhood of x does not meet A (otherwise x would be a limit point of A and hence in A). Thus this  -neighbourhood of x lies completely in X - A which is what we needed to prove.
-neighbourhood of x lies completely in X - A which is what we needed to prove.
( ) Conversely, suppose that X - A is open. We need to show that A contains all its limit points. So suppose x is a limit point of A and that x
) Conversely, suppose that X - A is open. We need to show that A contains all its limit points. So suppose x is a limit point of A and that x  A. Then x
A. Then x  X - A and hence has an
X - A and hence has an  -neighbourhood
-neighbourhood  X - A. But this is an
X - A. But this is an  -neighbourhood that does not meet A and we have a contradiction.
-neighbourhood that does not meet A and we have a contradiction.

Recap
The last two sections have shown how we can phrase the ideas of continuity and convergence purely in terms of open sets.
- A map f: X
 Y is continuous
Y is continuous  B open in Y
B open in Y  f -1(B) is open in X.
f -1(B) is open in X.
- A point x is a limit point of a subset A of X
 every open set containing x meets A (in a point
every open set containing x meets A (in a point 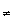 x).
x).
JOC February 2004
 R has no limit points.
R has no limit points. R2 | x2+ y2 < 1} form the closed disc {(x, y)
R2 | x2+ y2 < 1} form the closed disc {(x, y)  R2 | x2+ y2
R2 | x2+ y2 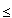 1}.
1}.
 -nd of x in X meets A in a point
-nd of x in X meets A in a point 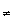 x.
x. ) Suppose A is closed. We need to show that X - A is open. So suppose that x
) Suppose A is closed. We need to show that X - A is open. So suppose that x  ) Conversely, suppose that X - A is open. We need to show that A contains all its limit points. So suppose x is a limit point of A and that x
) Conversely, suppose that X - A is open. We need to show that A contains all its limit points. So suppose x is a limit point of A and that x  A. Then x
A. Then x  Y is continuous
Y is continuous  B open in Y
B open in Y