Exercises 9

1. Prove that connectedness and compactness are topological properties. That is, they are both preserved by homeomorphism.

   Solution to question 1

2. If X is an infinite set with the discrete topology, which subsets of X are compact ?
   Give an example of a subspace of a metric space which is closed and bounded but not compact.

   Solution to question 2

3. Prove that any compact subset of a metric space is closed and bounded. Why does this not contradict the last question ?

   Solution to question 3

4. Prove that any space is compact under the cofinite topology. Is the same result true under the co-countable topology ?

   Solution to question 4

5. If A is a subset of R with its usual topology on which every continuous real-valued function is bounded, prove that A is compact.
   Consider the real line R with the topology generated by sets of the form (r, ) for r R. Prove that this last result fails.

   Solution to question 5

6. If f: C H is a continuous bijection from a compact space C to a Hausdorff space H prove that f is a homeomorphism.

   Solution to question 6

7. Define a metric on R by d(x, y) = |x - y| /(1 + |x - y|). Show that this metric is equivalent to the usual metric (i.e. the open sets are the same).
   Show that in this metric there are closed bounded subsets which are not compact. Why does this not contradict the Heine-Borel theorem ?

   Solution to question 7

8. Prove that if A and B are compact subspaces of a Hausdorff space then A B is compact.
   (In fact the Hausdorff condition is necessary though it's a bit tricky to find an example to prove it.)
   If A and B are compact is A 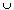B necessarily compact ?

   Solution to question 8

9. If A and B are subspaces of a metric space define d(A, B) to be the greatest lower bound of the set {d(a, b) | a A, b B}. If A and B are compact prove that d(A, B) = d(p, q) for some p A, q B.
   Show that if either A or B is non-compact this result may fail.

   Solution to question 9