Exercises 8

1. Prove that every subset of a Hausdorff space is Hausdorff in the subspace topology.
   
   1. If X and Y are Hausdorff, prove that X Y is Hausdorff.
      
   2. Prove or disprove: The image of a Hausdorff space under a continuous map is Hausdorff.
      
   3. If ~ is an equivalence relation on a Hausdorff space X, is the space X/~ with the identification topology always Hausdorff ?
      
   
   Solution to question 1

2. Show that the topology on R whose basis is the set of half-open intervals [a, b) is normal.

   Solution to question 2

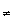3. A T₁ space is one in which for every pair of points x y there is an open set containing x but not y.
   Prove that a space is T₁ if and only if every singleton set {x} is closed.
   Prove that the only T₁ topology on a finite set is the discrete topology.

   Solution to question 3

4. Prove or disprove:
   
   1. The product of connected spaces is connected.
      
   2. If X is connected, then X/~ is connected (where ~ is an equivalence relation).
      
   
   Solution to question 4

5. Let Y be the space {a, b} with the discrete topology. Prove that a space X is connected if and only if the only continuous maps from X to Y are the two constant maps which map the whole of X to either a or b.

   Solution to question 5

6. If A is connected, prove that the closure cl(A) is also connected. Deduce that the components of a space are always closed subsets.
   Is the interior int(A) always connected ?

   Solution to question 6

7. Is the space R with the topology of Question 2 a connected space? What are its components?
   What are the components of R with:
   
   1. the co-finite topology,
      
   2. the co-countable topology.
      
   
   Solution to question 7

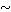8. If a, b are points in a topological space, define a b if there is a connected subset of X containing a and b. Prove that 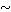is an equivalence relation.
   If a, b are points in a topological space, define a 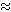b if there is a path in X connecting a and b. Prove that 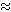is an equivalence relation.
   Deduce that pathwise connectedness implies connectedness.

   Solution to question 8