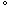Exercises 7

1. Make a twisted cylinder by gluing the (short) sides of a strip after a full (360 ) twist. Prove that the resulting space is homeomorphic to the cylinder (made by gluing the strip with no twist).

   Solution to question 1

2. Let S¹ be a circle in R² and let X be a cylinder S¹ [0, 1] with its subspace topology as a subset of R³. Let Y be the subset S¹ {0} of X and let Z be the subset S¹ {0, 1} of X.
   Describe the sets X / Y and X / Z with their identification topologies and identify them as more familiar topological spaces.
   What is the space X / S¹ {¹/₂} ?

   Solution to question 2

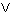3. Let X and Y be disjoint topological spaces with x a point in X and y a point in Y. Then the one-point union or wedge of X and Y, written X Y, is the space obtained by identifying the points x and y in X 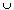Y. i.e. the space (X 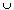Y)/{x, y}. Show that this space is homeomorphic to the subspace {x} Y X {y} of X Y.
   The smash product of spaces X and Y, written X Y, is the space X Y / X Y.
   Prove that the smash product of a circle S¹ with itself is homeomorphic to the sphere S² in R³.

   Solution to question 3

4. Define an equivalence relation on R with the usual topology by x ~ y if and only if x - y Q.
   Let p : R R/~ be the natural map. Show that the image of any open interval in R is the whole of R/~.
   If Y_x = p^-1({x}) for an equivalence class {x} in R/~ use the fact that any open set containing Y_x must contain an interval to deduce that the only open sets in R/~ with the identification topology are R/~ and .
   Hence show that R/~ with the identification topology is homeomorphic to R with the trivial topology.

   Solution to question 4

5. Make two surfaces A and B by joining two sheets of paper by twisted strips as shown below.

   

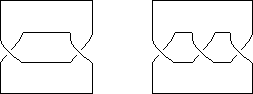
   What can you say about the spaces you get ?
   What would happen if we reversed the twist on one of the strips or if one of the strips was untwisted ?

   Solution to question 5