Exercises 6

1. If U A X, prove that U is closed in the subspace topology on A if and only if U = A Z for Z a closed subset of X.
   Prove or disprove the following:
   
   1. The interior of U in the subspace topology on A is equal to the interior of U in the topology on X,
      
   2. The closure of U in the subspace topology on A is equal to the closure of U in the topology on X.
      
   
   Solution to question 1

2. Let ₁ and ₂ be the subsets of the natural numbers N defined by:
   U ₁ if either U = or N - U is finite,
   U ₂ if either 1 U or N - U is finite.
   Prove that ₁ and ₂ are topologies on N.
   Let f be the identity map on N and let g be the map from N to N defined by
   g(n) = 1 if n is odd; g(n) = 1 + n/2 if n is even.
   Determine whether f and g are continuous either as maps from (N, ₁) to (N, ₂) or as maps from (N, ₂) to (N, ₁).

   Solution to question 2

3. Let A Y and B Y so that A B X Y. Prove that:
   
   1. cl(A) cl(B) = cl(A B)
      
   2. int(A) int(B) = int(A B)
      
   where cl denotes the closure and int denotes the interior.

   Solution to question 3

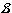4. A set of subsets of a topological space X is called a sub-basis for the topology if every open set can be written as a arbitrary union of finite intersections of sets in .
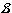   Show that a function f from a topological space X to a topological space Y is continuous if and only if f ^-1(U) is open for every set U in a sub-basis for the topology on Y.
   Prove that the set of all unbounded open intervals of R forms a sub-basis for the usual topology on R which is not a basis.
   Prove that a sub-basis of the product topology on X Y is the set of subsets of the form U Y and X V for U _X and V _Y .

   Solution to question 4

5. Prove that the set of all -neighbourhoods of rational points of R with also rational, forms a basis for the usual topology on R. Deduce that the usual topology on R has a countable basis. Prove that the discrete topology on R does not have a countable basis.

   Solution to question 5

6. Let X be the open unit square and let Y be the open unit quadrant, each with their topology as subsets of R². Prove that the map which takes the point (x, y) (in Cartesian co-ordinates) to (x, ¹/₂py) (in polar co-ordinates) is a homeomorphism.
   Prove that this homeomorphism cannot be extended to a homeomorphism between the closed unit square and closed unit quadrant.
   Show, however, that the closed unit square and closed unit quadrant are homeomorphic.

   Solution to question 6

7. Prove that [0, 1) (0, 1) and [0, 1) [0, 1] are homeomorphic subspaces of R².

   Solution to question 7