- the usual topology
- the discrete topology
- the trivial topology
- the cofinite topology [finite sets are closed]
- the co-countable topology [countable sets are closed]
- the topology in which intervals (x,
 ) are open
) are open
Solution to question 1
(This is the subspace topology as a subset of R with the topology of Question 1(vi) above.)
Find the interior and closure of the sets:
- {36, 42, 48}
- the set of even integers
Solution to question 2
(i) Prove that both Q and R - Q are dense in R with the usual topology.
(ii) Find all the dense subsets of N with the topology of the last question.
 B)
B)  cl(A)
cl(A)  cl(B) where cl indicates the closure.
cl(B) where cl indicates the closure.Give an example to show that equality might not hold.
Prove that int(A)
 int(B) = int(A
int(B) = int(A  B) and that int(A)
B) and that int(A) 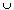 int(B)
int(B)  int(A
int(A 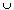 B) where int indicates the interior.
B) where int indicates the interior. Can this last inclusion ever be proper?
Show that there are 29 different topologies on the set {a, b, c}. How many of them are non-homeomorphic ?