Exercises 4

1. Prove that in a discrete metric space, every subset is both open and closed.
   If f is a map from a discrete metric space to any metric space, prove that f is continuous.
   Which maps from R (with its usual metric) to a discrete metric space are continuous ?

   Solution to question 1

2. If f from R to R is a continuous map, is the image of an open set always open ?
   Is the inverse image of a closed set always closed ?

   Solution to question 2

3. Show that in any metric space an -neighbourhood is an open set.
   Show that any open set can be written as a union of suitable -neighbourhoods.
   Give an example of an open subset of R (with its usual metric) which cannot be written as a union of finitely many -neighbourhoods.
   Can any open set can be written as a union of countably many suitable -neighbourhoods?

   Solution to question 3

4. If f is a continuous function from R² to R (usual metrics!) prove that the set
   { (x, y) R² | f(x, y) > 0 } is an open subset of R².
   Deduce that the open unit disc and open unit square are open sets.
   Is the set { (x, y) R² | f(x, y) 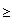0 } necessarily a closed set ?

   Solution to question 4

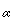5. If (a_i) is a sequence in a metric space convergent to a point , prove that 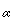is the only limit point of the set {a_i}. Give an example of a set with exactly two limit points. Give an example of a set with countably many limit points.

   Solution to question 5

6. Let X be the set {a, b, c, d, e}. Determine which of the following sets are topologies on X.
   
   1. = {X, , {a}, {a, b}, {a, c}}
      
   2. = {X, , {a}, {a, b}, {a, c, d}, {a, b, c, d}}
      
   3. = {X, , {a}, {a, b, c}, {a, b, d}, {a, b, c, d}}
      
   4. = {X, , {a}, {b}, {a, b}, {a, b, c}}
      
   
   Solution to question 6

7. Let be the set consisting of R, and all intervals of the form (q, ) with q Q. Show that is closed under all finite unions and intersections, but is not a topology on R.

   Solution to question 7

8. Let be the set consisting of N, and all subsets of N of the form {n, n+1, n+2, ...} for n N. Prove that is a topology on N. What are the closed subsets of N ?

   Solution to question 8

9. Let be the set of all subsets of R whose complements are countable, together with the empty set. Prove that is a topology on R. (This is called the co-countable topology.)

   Solution to question 9