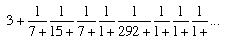 which is shorthand for
which is shorthand for 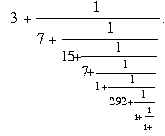
| Previous page (Cardinal numbers) | Contents | Next page (The Golden Ratio) |
You can think of calculating the decimal expansion of a (positive) real number as the result of implementing the algorithm:
(*) Make a note of the integer part of the number. Subtract this from the number.
This gives a number x in the range [0,1). If x ≠ 0 then:
** Multiply x by 10 **
This gives a number ≥ 0. Now repeat the loop from (*).
We can replace the step at ** ... ** by anything else that makes x bigger.
In particular, if we put in:
** Take the reciprocal 1/x of x **
then we get the Continued fraction expansion of x.
If you are lucky enough to have a calculator with a [1/x] button, then you can calculate this for (say) π = 3.141592654... and get the sequence 3, 7, 15, 1, 292, 1, 1, 1, ... which is written 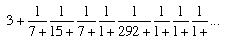 which is shorthand for
which is shorthand for 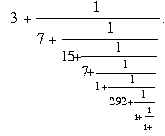
Truncating this at 3 + 1/7 gives the approximation 22/7 while truncating it at 3 + 1/7+1/15+1/1 gives the approximation 355/113 = 3.14159292... which is correct to 6 decimal places. It is a particularly good approximation since it stops just short of the rather large number: 292.
This was (amazingly) known to the Chinese mathematician Ch'ung Chi Tsu before 500 AD. Sadly, we don't know how he found it.
Continued fractions are used to get good rational approximations for real numbers.
You can use your calculator to experiment with some other real numbers.
For example, see what happens when you calculate the sequence for √2. From this, for example, one can get the approximation 89/70 for √2. (Note: (89/70)2 = 9801/4900 which is pretty close to 2.)
What you get if you start with (1 + √5)/2 is even more surprising.
In fact, you will find that the continued fraction expansion of the square root of any rational number is rather special.
Some of the famous irrational numbers have interesting continued fractions.
The Irish-born mathematician Lord Brouncker (1620 to 1684) found a continued fraction expansion:
The Swiss mathematician Leonhard Euler (1707 to 1783) found a continued fraction expression for e (the base of natural logarithms):
| Previous page (Cardinal numbers) | Contents | Next page (The Golden Ratio) |