
Given a rectangle with the property that when you remove a square from it, what is left has the same proportions as the original square, you may verify that this rectangle has the proportions φ : 1.
| Previous page (Continued fractions) | Contents | Next page (Space filling curves) |
The number (1 + √5)/2 = 1.6180339... that we met in the last supplement is what the Ancient Greeks called the Golden Ratio φ. In 1509 the mathematician Luca Pacioli (1445 to 1517) wrote a whole book: Divina proportione (= The divine proportion) about this number.
It occurs in many different places in mathematics.
The number φ satisfies the quadratic equation x2 - x - 1 = 0. A number of interesting identities follow from this. For example, 1/φ = φ - 1 = 0.6180339... and φ2 = φ + 1 = 2.6180339.... Hence φ3 = φ + φ2 = 1 + 2φ and so φ4= 2φ + 2φ2 = 2 + 3φ and in general φn = an + an+1φ where you might recognise the terms of the sequence (an). (See below.)

Given a rectangle with the property that when you remove a square from it, what is left has the same proportions as the original square, you may verify that this rectangle has the proportions φ : 1.
The Greeks used rectangles of this shape in many of their classical buidings since they believed such a shape was more aesthetically pleasing than any other rectangle.
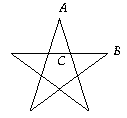
The Ancient Greeks investigated the geometry of the Pentangle:
They found that the ratio AB : AC is the Golden Ratio φ.
From this a modern mathematician can deduce that 2 cos(36°) = φ.
Since φ can be defined using the square root of a rational, one can construct lines whose lengths have ratio φ using ruler and compass constructions. Hence one may construct an angle of 36° by such a method and so construct a regular pentagon by ruler and compass constructions.
You saw on the last page that φ has the continued fraction expansion:
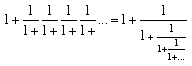
As this last result suggests, φ is closely related to the Fibonacci numbers. For example, the nth Fibonacci number fn = (φn - φ-n)/√5 and an even cuter formula is fn = [φn/√5] where [x] means the integer part of x.
This formula is named after the French mathematician Binet (even though de Moivre knew about it earlier).
| Previous page (Continued fractions) | Contents | Next page (Space filling curves) |