Continuity for Real functions

We now introduce the second important idea in Real analysis.

Continuity can be defined in several different ways which make rigorous the idea that a continuous function has a graph with no breaks in it or equivalently that "close points" are mapped to "close points".

For example, 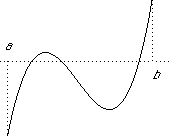is the graph of a continuous function on the interval (a, b)

while 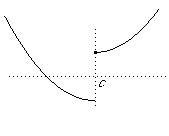is the graph of a function with a discontinuity at c.

To understand this, observe that some points close to c (arbitrarily close to the left) are mapped to points which are not close to f (c).

We will give a definition in terms of convergence of sequences and show later how it can be reformulated in terms of the above description.

Definition

A function f : R→ R is said to be continuous at a point p ∈ R if whenever (a_n) is a real sequence converging to p, the sequence (f (a_n)) converges to f (p).

Definition

A function f defined on a subset D of R is said to be continuous if it is continuous at every point p ∈ D.

Example

In the discontinuous function above take a sequence of reals converging to c from below. (That is, all the terms are < c.) Then the image of these gives a sequence which does not converge to f (c).

We also have the following.

Definition

A real valued function f defined on a subset S of R is said to be continuous if it is continuous at all points of S.

It will be easier to give (a lot of) examples of continuous functions after we have proved the following two results.

Definition

If f and g are functions from R to R, we define the function f + g by (f + g)(x) = f (x) + g(x) for all x in R.
Similarly we may define the difference, product and quotient of functions.

Theorem

If f and g are continuous a point p of R, then so are f + g, f - g, f.g and (provided g(p) ≠ 0) ^f /g .

Proof

This follows directly from the corresponding arithmetic properties of sequences.
For example: to prove that f + g is continuous at p ∈ R
Suppose (x_n)→ p. We are told that (f (x_n))→ f (p) and (g(x_n))→ g(p) and we must prove that (f + g)(x_n))→ (f + g)(p).
But the LHS of this expression is f (x_n) + g(x_n) and the RHS is f (p) + g(p) and so the result follows from the arithmetic properties of sequences.

Theorem

The composite of continuous functions is continuous.

Proof

Suppose f: R→ R and g: R→ R. Then the composition g f is defined by g f (x) = g(f (x)).
We assume that f is continuous at p and that g is continuous at f (p). So suppose that (x_i)→ p. Then (f (x_i))→ f (p) and then (g(f (x_i)))→ g(f (p)) which is what we need.

Examples

1. Clearly the identity function which x ↦ x is continuous.
   Hence, using the above, any polynomial function is continuous and hence any rational function (a ratio of polynomial functions) is continuous at any point where the denominator is non-zero.

2. We will see later that functions like √, sin, cos, exp, log, ... are continuous. It follows that , for example sin²(x + 5), exp(-x²), √(1 + x⁴), ... are continuous since they are made by composing continuous functions.
   

---

Previous page (Cauchy sequences)

Contents

Next page (Limits of functions)

---

JOC September 2001