Convergence in a metric space

Just as a convergent sequence in R can be thought of as a sequence of better and better approximtions to a limit, so a sequence of "points" in a metric space can approximate a limit here.

Definition

A sequence (x_n) of points in a metric space (X, d) converges to a limit α if the real sequence (|d(x_n, α)| converges to 0 in R.

Remark

If you insist on "back to basics" this reads:
Given ε > 0 there exists N ∈ N such that if n > N then we have d(x_n, α) < ε.

Examples

1. For R with its usual metric this is the same as before.

2. In C with the metric d(z, w) = |z - w|, consider the sequence (z, z², z³, ...) with |z| < 1.
   Then this sequence converges to 0 ∈ C.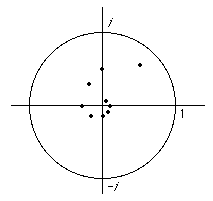

   

   e.g. Take z = ⁽¹⁺ⁱ⁾/₂ so that |z| = ¹/_√2
   

   
   The points lie on a spiral.
   
   

   Proof that the sequence converges

   Look at the real sequence (d(x_n, 0)) = (|zⁿ- 0|) = (|z|ⁿ)→ 0 since |z| < 1.
   
   
   

3. Look at the sequence in R² given in the following way.
   x₁= 2√3, y₁= 3 and then define the later terms by 2/x_n+1= 1/x_n+ 1/y_n and y_n+1= √(x_n+1y_n).
   This gives a sequence which evaluates numerically to:
   ( (3.4642, 3.0000), (3.2154, 3.1057), (3.1596, 3.1325), (3.1460, 3.1392), (3.1426, 3.1408), 3.1418, 3.1414), ...)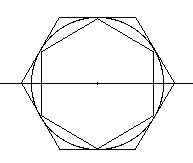

   

   This sequence is based on the method used by Archimedes to calculate π.
   Start with x₁= the semiperimeter of the "outside hexagon"
   Start with y₁= the semiperimeter of the "inside hexagon"
   and then double the number of sides to get a 12-gon , a 24-gon, etc.
   Archimedes took the calculation up to n = 5 (corresponding to a 96-gon).

   In fact the sequence in R² converges to the point (π, π).
   

This last result suggests the following.

Theorem

Convergence in R² with its usual metric d₂ is "componentwise".

That is ((x₁ , y₁), (x₂ , y₂), ... )→ (α , β) if and only if
(x₁ , x₂ , ... )→ α and (y₁ , y₂ , ... )→ β.

Proof

( ⇒ ) Given ε > 0 we know that we have N so that if n > N then √(|x_n- α|²+ |y_n- β|²) < ε. But then we must have |x_n- α| < ε and so (x_n)→ α. Similarly for the other component.

Conversely: Given ε > 0 choose N so that if n > N then |x_n- α| < ε and |y_n- β| < ε. But then √(|x_n- α|²+ |y_n- β|²) < √(ε²+ ε²) = √2 ε and so we may make this as small as we like.

In fact this last result holds for any finite-dimensional space Rⁿ and also holds for such spaces with any of the metrics d_p. The situation for infinite-dimensional spaces of sequences or functions is different as we will see in the next section.