Convergence in infinite dimensional spaces

We will consider some more examples of convergence in metrics.

First, we look at some examples of convergence in spaces of sequences.

1. Let X be the set of all bounded real sequences with the metric d_∞ defined earlier.
   Take the sequence of "points" in X (that is, a sequence of sequences) given by:

   x₁ = (¹/₁ , ¹/₂ , ¹/₃ , ... ), x₂ = (¹/_1² , ¹/_2² , ¹/_3² , ... ), x₃ = (¹/_1³ , ¹/_2³ , ¹/_3³ , ... ) , ...
   Then this sequence of sequences converges to the sequence y = (1 , 0 , 0 , 0 , ... ) in d_∞.

   Proof
   d_∞(x_n, y) = lub { 0 , ¹/_2ⁿ, ¹/_3ⁿ, ... } = ¹/_2ⁿand this is small when n is large.
   
   
   

2. This next example shows one of the differences between the finite and infinite-dimensional cases.

   Take the sequence in X given by:

   x₁ = (1 , 0 , 0 , ... ), x₂ = (0 , 1 , 0 , ... ), x₃ = (0 , 0 , 1 , 0 , ... ), ...
   Then although the "sequence of first components", the "sequence of second components", the "sequence of third components", ... all converge to 0, the sequence x_n does not converge to the zero sequence: 0, since d_∞(x_n, 0) = 1 for all n.

   So the theorem proved for finite dimensional spaces in the last section does not hold for this infinite dimensional space.
   

3. Define a sequence of functions in C[0, 1] by f₁(t) = t , f₂(t) = t/₂ , f₃(t) = t/₃ , ...
   We claim that this sequence converges to the 0-function in the metric d_∞.

   Proof
   The maximum of the function |f_n(x) - 0| is at x = 1 and is ¹/_n. Thus the real sequence (d_∞(f_n, 0))→ 0 and so the 0-function is the limit.
   
   
   Remarks
   
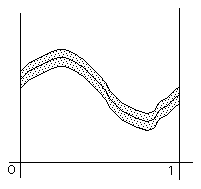
   We can get a "picture" of what convergence in the metric d_∞ "Looks like".
   Given a function g on (say) [0, 1], we can draw "An ε-band" around its graph.

   Then a function is within ε of g provided its graph lies in this ε band.

   Thus a sequence (f_n)→ g in d_∞ if the graphs of every function "far enough down" the sequence lie in an arbitrarily small ε band.
   
   

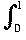4. This time we consider converence in the d₁ metric given by d₁(f, g) = |f (x) - g(x)|dx. (i.e. the "distance between the functions is the area between their graphs").
   
   
   1. The picture above shows that the sequence of functions (x/_n) converges to the 0-function.
      

   2. Here is a curious sequence of "spike functions"
      

      
      Define f_n(x) by:

      Then (f_n)→ the 0-function in the metric d₁.
      
      
      Proof
      d₁(f_n, 0) = the area under the curve = ¹/_n and so (d₁(f_n, 0))→ 0 and the sequence converges.
      
      Note however, that this sequence does not converge to the 0-function in d_∞ since the graph of f_n "sticks out" of any small ε band of the 0-function.

      Thus it can happen that a sequence which converges in one metric may fail to converge in another.
      

1. Convergence of sequences of functions in the metric d_∞ is particularly important. It is called uniform convergence and it turns out that this convergence has particularly nice properties, particularly in relation to differentiation and integration.

2. Convergence of sequences of functions in the metric d₁is also important. It is called convergence in the mean (because in some sense it "Averages out" the distance between functions). It is important in some applications. For example, the partial sums of the Fourier series of a function converges to the function in the mean.

3. The most obvious way of considering convergence of a sequence of functions is pointwise convergence. That is, a sequence (f_n) of functions in (say) C[0, 1] is pointwise convergent to f if at each x ∈ [0. 1], the real sequence (f_n(x)) converges in R to f (x).
   For example, the pointwise limit of the sequence of "spike functions" above is the function defined by f (¹/₂) = 1 and f (x) = 0 otherwise.