Some of the other metrics we have considered give some similar unpleasant results.
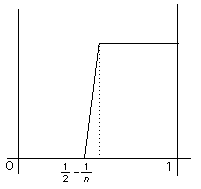
For example, consider the sequence of functions (fn) where fn is:
| Previous page (Convergence in infinite dimensional spaces) | Contents | Next page (The Weierstrass approximation theorem) |
We recall that uniform convergence is convergence in the metric d∞ on a space of functions.
Some of the examples we considered in the last section show that it is possible for a sequence of continuous functions to be pointwise convergent to a non-continuous function.
Some of the other metrics we have considered give some similar unpleasant results.

For example, consider the sequence of functions (fn) where fn is:
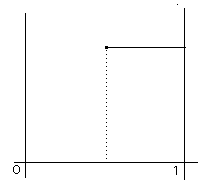
Then the pointwise limit of (fn) is the function f given by f (x) = 0 if x < 1/2 and f (x) = 1 otherwise. Its graph is:
Then it is easy to see that d1(fn, f) = 1/2n→ 0 as n→ ∞. Unfortunately, f does not lie in C[0, 1] and so we cannot quite talk about convergence in this space. However, the sequence (fn) is a Cauchy sequence in C[0, 1] with the metric d1.
This motivates:
Definition
Remarks
The nice thing about the metric d∞ is:
Theorem
First we show that the sequence converges to its pointwise limit in the metric d∞.
Proof of that
Take a point x ∈ [0, 1]. Then the sequence (fn(x)) is a real sequence which, from the fact that (fn) is a Cauchy sequence, is a Cauchy sequence in R and hence has a limit which we will call f (x). Thus the pointwise limit f is defined.
Since at each point fn(x) is close to f (x) we have the lub{ |fn(x) - f (x)| for x ∈ [0, 1] } is small and so (fn)→ f in d∞.
The last thing we need to prove is that the pointwise limit f is continuous.
Proof of that
To prove that f is continuous at p ∈ [0, 1], take some ε > 0. Choose N such that d∞(fn, f) < ε.
Then since fn is continuous, there exists δ such that if x is in the interval (p - δ, p + δ) then |fn(x) - fn(p)| < ε. Then |f (x) - f (p)| = |f (x) - fn(x) + fn(x) - fn(p) + fn(p) - f (p)| < |f (x) - fn(x)| + |fn(x) - fn(p)| + |fn(p) - f (p)| < ε + ε + ε and so can be made arbitrarily small.

| Previous page (Convergence in infinite dimensional spaces) | Contents | Next page (The Weierstrass approximation theorem) |