MT2002 Analysis
Some logic
Definition
A proposition is a statement which can be either TRUE or FALSE.
For example, the proposition P = " 2 + 2 = 4 " is true, while Q = " There is a real number x such that x2 = -1 " is false.
If P and Q are propositions then the proposition P 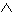 Q (read P and Q) is true if both P and Q are true and false otherwise.
Q (read P and Q) is true if both P and Q are true and false otherwise.
The proposition P 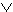 Q (read P or Q) is true if either P or Q (or both) are true and is false otherwise.
Q (read P or Q) is true if either P or Q (or both) are true and is false otherwise.
The proposition ¬P (read not P) is true if P is false and is false if P is true.
The proposition P ⇒ Q (read P implies Q or if P then Q) is only false if P is true and Q is false and is true otherwise.
In particular, if P and Q are both false then P ⇒ Q is true.
The proposition P ⇔ Q (read P is equivalent to Q or P if and only if Q) is true if either both P and Q are true or both P and Q are false and is false otherwise.
The English mathematician George Boole (1815 to 1864) noticed that arguments involving propositions could be reduced to set theory. In particular, any argument involving three propositions or less can be proved using a Venn diagram -- invented by the English mathematician John Venn (1834 to 1923).
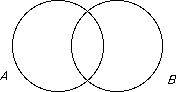
If we take a Venn diagram involving sets A and B and take the proposition P to be "The point x ∈ A" and Q to be "The point x ∈ B" then P 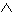 Q is the proposition "The point x ∈ A ∩ B" and P
Q is the proposition "The point x ∈ A ∩ B" and P 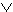 Q is the proposition "The point x ∈ A ∪ B".
Q is the proposition "The point x ∈ A ∪ B".
Many of the propositions we will encounter in this course are constructed using the quantifiers ∀ and ∃.
The symbol ∀ stands for for all or for every or for each ...
The symbol ∃ stands for there exists or there is a or for some ...
To make the expressions easier to interpret we can put in some such that's or something similar.
We can combine these with other expressions, as for example:
(∀ m∈ N) (∃ n ∈ N) (n > m)
which we can read as:
For every integer m there is some integer n such that n > m.
This is true since we can take (say) n = m + 1.
However, the statement:
(∃ n∈ N) (∀ m ∈ N) (n > m)
which we can read as:
There is some integer n such that for every integer m we have n > m
is false since there is no integer which is bigger than every integer.
Note that in the first of these two expressions, the m which we need to find to show that the expression is true can depend on n, but in the second, because the ∃ comes before the ∀, we have to find an m which does not depend on a particular n.
So the order in which the quantifiers are written is important.
JOC September 2001
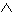 Q (read P and Q) is true if both P and Q are true and false otherwise.
Q (read P and Q) is true if both P and Q are true and false otherwise.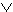 Q (read P or Q) is true if either P or Q (or both) are true and is false otherwise.
Q (read P or Q) is true if either P or Q (or both) are true and is false otherwise.