Rationals and irrationals

Definition

The rational numbers Q are all fractions ^a/_b with a, b integers.

Theorem

If r, s are rationals, so are r + s, r - s, r × s and (if s ≠ 0) ^r /s .

Proof

An exercise in arithmetic with fractions.

Theorem

The real number √2 is not a rational number.

Proof

(By contradiction) Suppose that √2 = ^a/_b for a, b ∈ Z. We may as well assume that a, b have no common factors else we could cancel them out.
Then 2b² = a² and so a is even. But then a² is divisible by 4 and so b² is even. But then b is even and so a and b do have a common factor. Thus we have a contradiction.

An aside on decimals

Decimals were first introduced into Europe by the Flemish/Belgian mathematician Simon Stevin (1548 to 1620) though they had been used earlier by some Indian, Arabic and Chinese mathematicians.

Some facts about decimals

Every real number has a unique decimal expansion -- except that terminating decimals (which end in ...00000...) can also be expanded to finish in ... 99999 ...
For example, 1 = 1.0000 ... = 0.9999... , ¹/₄ = 0.250000 ... = 0.249999 ... , etc.
Numbers with such terminating decimal expansions are of the form ^m/_n with the denominator n having 2 or 5 as its only prime factors.

Rational numbers have decimal expansions which repeat periodically.
For example ¹/₆ = 0.166666 ... which we write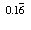
while ¹/₇ = 0.14285714285 ... =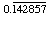
The recurring decimal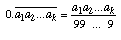
For example 0.123123 ... = ¹²³/₉₉₉ = ⁴¹/₃₃₃ .
An irrational number like √2 has a decimal expansion which does not repeat:
√2 = 1.4142135623730950488016887242096980785696718753769480731766797379907324784621070 ...