Functions

One of the important things we will consider in this course is the idea of a function (most often from R to R). It took a long time for mathematicians to work out exactly what should be meant by such a thing.

You can see some of the early attempts.

As far as we are concerned a map or function f : A→ B is a method of assigning to every (*) element a ∈ A a unique (*) element f(a) ∈ B.
To do this rigorously (we will not, mostly) you can define a function f to be a subset of A × B (which looks a lot like the graph of the function) and include rules which ensure the two properties (*) above hold.

Definitions

A map is one-one (or injective) if two distinct elements of A never map to the same element of B.
That is, f: A→ B is one-one if (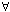x, y ∈ A)(f (x) = f (y) ⇒ x = y)

A map is onto (or surjective) if every element of B has some element of A mapped to it.
That is, f: A→ B is onto if (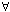y ∈ B)(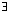x ∈ A)(f (x) = y)

A map which is both one-one and onto is called a one-one correspondence (or bijection).

The set A is called the domain of the map f : A→ B and the set B is sometimes called the codomain of f.

The set of all b ∈ B with f (a) = b for some a ∈ A is called the image (or range) of f.