Definition
We will see later that many infinite sets are countable but that some are not.
Some versions of the above definition include finite sets among the countable ones, but we will (mostly) not do so.
- The set Z of (positive, zero and negative) integers is countable.
Proof
Here is a counting. That is, we list the elements
N 1 2 3 4 5 6 7 ... Z 0 1 -1 2 -2 3 -3 ...
You can (if you wish) write down a formula: 1/2 n if n is even, 1/2 (n - 1) if n is odd.

- The set N × N is countable.
Proof
Count the points with integer coefficients in the positive quadrant as shown. (The formula is now rather tricky to write down.)
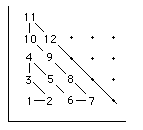

- The set Q of all rationals is countable.
Proof
Write down a positive rational x/y at the point (x, y) in the plane and count as in the last example, except that you can leave out a point if you have already counted the rational. You have to do this because, for example, 1/1 = 2/2 etc.
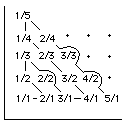
This will count all the positive rationals. Then use the same trick as in example 1 to count all the rationals.

The amazing insight achieved by Cantor is the following result.
This proof is called the Cantor diagonalisation argument.
Suppose we could write down all the decimal expansions of the reals in (0, 1) in a list:
0.a1a2a3a4a5...
0.b1b2b3b4b5...
0.c1c2c3c4c5...
0.d1d2d3d4d5...
...
and now define a decimal x = x1x2x3x4... by x1≠ a1 (or 9), x2≠ b2 (or 9), x3≠ c3 (or 9), etc.
Then the decimal expansion of x does not end in recurring 9's and it differs from the nth element of the list in the nth decimal place. Hence it represents an element of the interval (0, 1) which is not in our counting and so we do not have a counting of the reals in (0, 1).

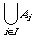 is finite or countable.
is finite or countable.