We saw before that the Real numbers R have some rather unexpected properties. In fact, there are many things which it is difficult to prove rigorously.
Examples
- How do we know that √2 exists? In other words how can we be sure that there is some real number whose square is 2?
It is easy to convince yourself that (say) 2 + 3 = 3 + 2. How about √2 + √3 = √3 + √2 or e +π = π + e?
- One's intuition about what should be true works pretty well for N or Z or even for Q. Things don't get hard until we are forced (like the Pythagoreans) to admit the existence of irrationals.
There are constructive methods for making the full set R from Q and hence starting with N. The first rigorous construction was given by Richard Dedekind (1831 to 1916) in 1872.
You can see more about Dedekind's construction.
However, for the moment we will simply give a set of axioms for the Reals and leave it to intuition that there is something that satisfies these axioms.
We start with a set, which we'll call R and a pair + . of binary operations.
The Axioms
- These are divided into three groups.
- I The algebraic axioms
- R is a field under + and .
This means that (R, +) and (R, .) are both abelian groups and the distributive law (a + b)c = ab + ac holds.
- II The order axioms
- There is a relation > on R.
(That is, given any pair a, b then a > b is either true or false).
It satisfies:
a) Trichotomy: For any a ∈ R exactly one of a > 0, a = 0, 0 < a is true.
b) If a, b > 0 then a + b > 0 and a.b > 0
c) If a > b then a + c > b + c for any c
Something satisfying axioms I and II is called an ordered field.
- Examples
- A subset A which has a lower bound has a greatest lower bound.
Proof
Let B = {x ∈ R | -x ∈ A}. Then B is bounded above by -(the lower bound of A) and so has a least upper bound b say. It is then easy to check that -b is a greatest lower bound of A.

- The Archimedean property of the Reals
If a > 0 in R, then for some n ∈ N we have 1/n < a.
Equivalently: Given any x ∈ R, for some n ∈ N we have n > x.
Proof
This last statement is equivalent to saying that N is not bounded above. This seems like a very obvious fact, but we will prove it rigorously from the axioms.
Suppose N were bounded above. Then it would have a least upper bound, M say. But then M - 1 is not an upper bound and so there is an integer n > M - 1. But then n + 1 > M contradicting the fact that M is an upper bound.
Remark
This result has been attributed to the great Greek mathematician (born in Syracuse in Sicily) Archimedes (287BC to 212BC) and appears in Book V of The Elements of Euclid (325BC to 265BC).
From this we can deduce :
- Between any two real numbers is an rational number.
Proof
Let a ≠ b be real numbers with (say) a < b. Choose n so that 1/n < b - a. Then look at multiples of 1/n. Since these are unbounded, we may choose the first such multiple with m/n > a.
We claim that m/n < b. If not, then since (m-1)/n < a and m/n > b we would have 1/n > b - a.

Remark
A set A with the property that an element of A lies in every interval (a, b) of R is called dense in R.
We have just proved that the rationals Q are dense in R. In fact, the irrationals are also dense in R.
We can now prove the result we stated earlier.
- The real number √2 exists.
Proof
We will get √2 as the least upper bound of the set A = {q ∈ Q | q2 < 2 }. We know that A is bounded above (by 2 say) and so its least upper bound b exists by Axiom III.
We now prove that b2 < 2 and b2 > 2 both lead to contradictions and so we must have b2 = 2 (by the Trichotomy rule).
So suppose that b2 > 2. Look at (b - 1 /n )2 = b2 - 2b /n + 1 /n2 > b2 - 2b/n.
When is this > 2 ?
Answer: When b2 - 2b/n > 2 which happens if and only if b2 - 2 > 2b/n or 1/n < (b2 -2)/2b and we can choose such an n by the Archmedean property. Thus b - 1/n is an upper bound, contradicting the assumption that b was the least upper bound.
Similarly, if b2 < 2 then (b + 1/n)2 = b2 + 2b/n + 1/n2 > b2 + 2b/n.
Can this be < 2 ?
Answer: Yes, when b2 + 2b/n < 2 which happens if and only if 2 - b2 > 2 b/n or 1/n < (2 - b2)/2b and we can choose an n satisfying this, leading to the conclusion that b would not be an upper bound.

- Real numbers can be defined by decimal expansions.
Proof
Given the decimal expansion (say) 0.a1a2a3... consider the set (of rationals) {0.a1 , 0.a1a2 , 0.a1a2a3 , ...} = { a1/10 , (10 a1 + a2)/100 , (100 a1 + 10 a2 + a3)/1000 , ... }.
This is bounded above -- say by (a1+ 1)/10 or by (10 a1+a2+ 1)/100 etc. and so it has a least upper bound.
This is the real number defined by the decimal expansion.



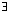 b ∈ R)(
b ∈ R)(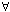 x ∈ A)(b ≥ x) ⇒ b ≥ M
x ∈ A)(b ≥ x) ⇒ b ≥ M