Convergence in the Reals

One of the two most important ideas in Real analysis is that of convergence of a sequence.

Definition

A sequence in R is a list or ordered set: (a₁ , a₂ , a₃ , ... ) of real numbers.

Examples

One may define a sequence (a_n) by giving an explicit formula for the nth term.

1. (¹/_n) = ( 1 , ¹/₂ , ¹/₃ , ... )

2. (sin(^πn/₄)) = (¹/_√2 ,1 , ¹/_√2 , 0 , -¹/_√2 ,-1 , -¹/_√2 , 0 , ... )

3. ( ⁽⁵ⁿ⁺²⁾/_(3n+1) ) = ( ⁷/₄ , ¹²/₇ , ¹⁷/₁₀ , ²²/₁₃ , ²⁷/₁₆ , ... )
   

One may define a sequence by a recurrence relation. This gives a formula for the nth term in terms of earlier ones.

4. a_n+1 = a_n/(a_n+ 1), a₁ = 1.
   This gives the sequence ( 1 , ¹/₂ , ¹/₃ , ¹/₄ , ... ).

5. f_n+2 = f_n+1 + f_n and f₁ = f₂ = 1.
   This gives (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... )

   This is the Fibonacci sequence first introduced by the Italian mathematician Fibonacci or Leonard of Pisa (1170 to 1250) and much studied by Edouard Lucas (1842 to 1891).

6. a_n+1 = (a_n+ 2/a_n)/2 and a₁ = 1.
   This gives ( 1 , ³/₂ , ¹⁷/₁₂ , ⁵⁷⁷/₄₀₈ , ⁶⁶⁵⁸⁵⁷/₄₇₀₈₃₂ , ... ) which is approximately ( 1, 1.5, 1.41667, 1.414215, 1,414213562, ... )

   This is the result of applying Newton's method for solving an equation to x² = 2 and hence gives a method of calculating √2.

7. a_n+1 = a_n + 1/n² and a₁ = 0.
   This gives the sequence ( 0 , 1 , ⁵/₄ , ⁴⁹/₃₆ , ²⁰⁵/₁₄₄ , ⁵²⁶⁹/₃₆₀₀ , ... ) which is approximately ( 0, 1, 1.25, 1.3611, 1.423611, 1.463611, ... )
   These are the partial sums of the series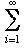 (¹/_i²) which the Swiss mathematician Leonhard Euler (1707 to 1783) proved "settles down" to 1.6449... = π²/₆.
   

One may think of a sequence as being used to approximate a real number which might be difficult to get hold of directly. For example, the sequence 6) above gives approximations to the number √2.

The main thing to remember is:

Informal definition

A real sequence ( a_n) is said to be convergent to a limit α if all the terms of the sequence become close (*) to α for n large (**).

To formalise the idea at (*), we mean that if we are given any small error ε then the terms of the sequence are within ε of α provided n is big enough. By big enough (**) we mean that we can find some N so that this happens when n > N.

We get the rigorous statement corresponding to the above:

Definition

A real sequence ( a_n) converges to a limit α if:
given ε > 0, there exists N ∈ N such that if n > N then | a_n- α | < ε.

Remarks

1. The N that it is necessary to choose will depend on what ε you are using. In general, the smaller the ε the bigger you will have to choose N.
   
2. Note that all the terms a_n with n > N must approximate α to better than ε.
   
3. In terms of quantifiers we may express this as:
   A sequence (x_i)→ α if (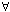ε > 0) (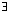N ∈ N)( 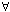n > N)(|x_n - α| < ε)
   Note that since the "(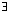N ∈ N)" occurs after the "(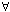ε > 0)" the value of N that we must find is allowed to depend upon ε.
   
4. A sequence which does not converge is called divergent.
   

Examples

1. The sequence ( 1 , ¹/₂ , ¹/₃ , ... ) is convergent to 0.

   Proof
   Given ε use the Archimedian property to choose N with ¹/_N≤ ε. Then if n > N we have ¹/_n < ¹/_N ≤ ε.
   
   

2. The sequence ( 1, 2, 3, 4, ... ) is not convergent (to any limit).

   Proof
   We will see later than any unbounded sequence does not converge.
   
   
   

3. The sequence (1, ³/₂ , ¹¹/₆ , ²⁵/₁₂ , ¹³⁷/₆₀ , ⁴⁹/₂₀ , ... ) = (1 , 1 +¹/₂ , 1 +¹/₂+¹/₃ , 1 +¹/₂+¹/₃+¹/₄ , ... ), where a_n= 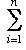(¹/_i), is not convergent.

   Proof
   The terms of this sequence are the partial sums of the harmonic series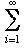 (¹/_i). This result was first proved by Jacob Bernoulli (1654 to 1705)
   Group the terms of the series in the following way.
   1 + ¹/₂ + (¹/₃+¹/₄) + (¹/₅+¹/₆+¹/₇+¹/₈) + (¹/₉+¹/₁₀+ ... +¹/₁₆) + ...
   and these terms are bigger than the terms of
   1 + ¹/₂+ (¹/₄+¹/₄) + (¹/₈+¹/₈+¹/₈+¹/₈) + (¹/₁₆+¹/₁₆+ ... +¹/₁₆) + ... = 1 + ¹/₂ + ¹/₂ + ¹/₂ + ...
   and the partial sums of this series are clearly unbounded.
   
   
   

4. The sequence ( 1, 0, 1, 0, 1, 0, 1, 0, ... ) is not convergent even though it is bounded.
   

---

Previous page (Axioms for the Real numbers)

Contents

Next page (Some properties of convergent sequences)

---

JOC September 2001