MT2002 Analysis
Analysis Summary
Set theory
Rational numbers Q are fractions { a/b | a, b ∈ Z}.
√2 is an irrational number.
Every Real number has a unique decimal expansion (up to the ambiguity of ending in ...000... or ...999...).
Rational numbers have terminating or recurring decimal expansions.
A set which can be put into one-one correspondence with N is called countable.
Countable sets: Z, N × N, Q, ...
The Cantor diagonalisation argument shows that R is uncountable.
Subsets of countable sets are either finite or countable.
A countable union of countable sets is countable.
The Real numbers
The set of Real numbers satisfies the properties:
I (Algebraic axiom) R is a field under + and . .
II (Order axioms) There is a relation > on R satisfying:
(a) for any a ∈ R, exactly one of 0 > a, a = 0, a > 0 is true (Trichotomy),
(b) if a, b ∈ R with a, b > 0 then a + b > 0 and a b > 0,
(c) if a, b, c ∈ R and a > b then a + c > b + c.
III (Completeness axiom) Any bounded set has a least upper bound.
From these one may deduce:
(The Archimedean property) If a > 0 in R then for some n ∈ N we have a > 1/n > 0.
There is a rational number between any two real numbers.
Convergence in the Real numbers
A sequence (a1 , a2 , a3 , ... ) converges to a limit α if:
Given ε > 0 there exists N ∈ N such that for n > N we have | an - α | < ε.
Properties of convergence
Any convergent sequence is bounded (above and below).
Arithmetic properties: If (an)→ α and (bn)→ β are convergent sequences, then (an + bn)→ α + β, (an - bn)→ α - β, (anbn)→ αβ, and, provided that bn , β ≠ 0 , (an/bn)→ α/β.
A sequence (an) for which an+1 ≥ an for all n, is called monotonic increasing.
A bounded monotonic increasing sequence converges to its least upper bound.
(Bolzano-Weierstrass theorem) Any bounded sequence contains a convergent sub-sequence.
A sequence (a1 , a2 , a3 , ... ) is called a Cauchy sequence if:
Given ε > 0 there exists N ∈ N such that for m, n > N we have | am - an| < ε.
Cauchy sequences in R are convergent.
Continuity for Real functions
A function f : R→ R is said to be continuous at p ∈ R if:
Whenever (xn) is a sequence converging to p, the sequence ( f (xn) ) converges to f (p).
One may prove that this definition is equivalent to the ε-δ definition:
A function f : R→ R is said to be continuous at p ∈ R if:
Given ε > 0 there is a δ > 0 such that if | x - p | < δ then | f (x) - f (p) | < ε.
A function which is continuous at every point of R is called a continuous function.
If f and g are functions continuous at p, so are f + g, f - g, fg, and (provided that g(p) ≠ 0) f / g.
If f is continuous at p and g is continuous at f (p) then the composite function h(x) = g  f (x) = g (f (x)) is also continuous at p.
f (x) = g (f (x)) is also continuous at p.
Metric spaces
A metric space is a set X together with a function d from X × X to R satisfying the properties:
(a) d(x, y) ≥ 0 and d(x, y) = 0 if and only if x = y,
(b) d(x, y) = d(y, x)
(c) d(x, y) + d(y, z) ≥ d(x, z) (the triangle inequality).
The space R2 is a metric space under the metrics:
d2((x1, y1), (x2, y2)) = √((x1 - x2)2+ (y1 - y2)2) (The usual or Pythagorean metric)
d1((x1, y1), (x2, y2)) = |x1 - x2| + |y1 - y2| (The taxicab metric)
d∞((x1, y1), (x2, y2)) = max {|x1 - x2|, |y1 - y2|} (The supremum or uniform metric).
The space B[0, 1] of bounded functions on the interval [0, 1] is a metric space under the metric:
d∞((xi), (yi)) = max {|x1 - y1|, |x2 - y2|, ... } (The uniform metric).
The space C[0, 1] of continuous functions on the interval [0, 1] is a metric space under the metrics:
d∞(f, g) = lub {|f (x) - g(x)| | x ∈ [0, 1]} (The uniform or supremum metric).
d1(f, g) = 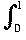 |f (x) - g(x)| dx.
|f (x) - g(x)| dx.
Convergence in a metric space
A sequence (xn) of points in a metric space (X, d) converges to a point α in X
if the real sequence (d(xn, α)) converges to 0 in R.
Equivalently: if given ε > 0 there exists N ∈ N such that for n > N we have d(xn, a ) < ε.
Convergence in the metric d∞ is called uniform convergence. It is possible for sequences in spaces of sequences or functions to converge in one metric but not in others.
A space is called complete if every Cauchy sequence has a limit. The space C[0, 1] is a complete space under the metric d∞ but not under the metric d1.
Further properties of continuous functions
The Weierstrass approximation theorem states that every continuous function on a closed bounded interval is the uniform limit of polynomial functions
The Intermediate Value theorem states that a function which is continuous on an interval and which is positive at some point and negative at another must be 0 somewhere on the interval.
A continuous function on a closed bounded interval is bounded and attains its bounds.
JOC September 2001
 f (x) = g (f (x)) is also continuous at p.
f (x) = g (f (x)) is also continuous at p.
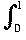 |f (x) - g(x)| dx.
|f (x) - g(x)| dx.