Exercises 10

1. If f, g are continuous functions on an interval [a, b], prove that d₁(f, g) ≤ (b - a)d_∞(f, g).
   Hence prove that if a sequence (f_n) in C[a, b] converges to a function f in d_∞ it also converges to f in d₁.

   Solution to question 1

2. Let f be a continuous function on the interval [0,1] for which f (0) = f (1). By considering the function h(x) = f (x) - f (x + ¹/₂) on a suitable interval, prove that there is some point x in [0, ¹/₂] for which f (x) = f (x + ¹/₂).
   Deduce that there are two points opposite one another on the equator where the temperature is the same.

   Solution to question 2

3. Let f be a function from R to R for which there is a constant λ < 1 such that | f (x) - f (y) | ≤ λ| x - y|. Such a function is called a contraction mapping.
   Choose a point x₀ and define a sequence (a_n) by a₁= x₀, a_n+1= f (a_n) for n ≥ 1. Prove that this is a Cauchy sequence and that it has a limit a which is a fixed point of f. i.e. f (a) = a.
   Prove that this fixed point is unique.

   Solution to question 3

   The next three questions try to show you why the metric d₂ is an easier one to work with than d₁ or d_∞.
   
   

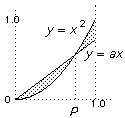
4. Find the best-fit straight-line through the origin to the function x² in the metric d₁.
   i.e find the value of a which minimises d₁(x², ax).
   For this you have to minimise the shaded area.
   Calculate this area by first finding the x-coordinate of the point P in terms of a.
   
   

   Solution to question 4

   
   

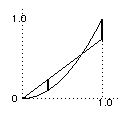
5. Find the best-fit straight-line through the origin to the function x² in the metric d_∞.
   i.e. find the value of a which minimises d_∞(x², ax).
   For this you have to choose a so that the "vertical distance between the graphs" is a minimum.
   From the picture, you can see that the best you can do is to adjust the value of a so that the two dark lines have equal length.
   
   

   Solution to question 5

6. Use the method of Exercises 9 Question 1 to find the best-fit straight-line through the origin to the function x² in the metric d₂.

   Solution to question 6