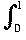Exercises 9

1. Define the metric d₂ on the space C[0,1] of continuous functions on [0,1] by d₂(f,g) =[(f (x) - g(x))²dx]^1/2.
   If a, b are fixed real numbers, calculate d₂(x², ax + b). Use the usual method for finding the turning points of a function of two variables to find the values of a, b for which this distance is a minimum.
   [This is the process of linear regression which is important in many areas of applied mathematics and statistics.]

   Solution to question 1

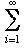2. Let (f_n) be a sequence of continuous functions on a bounded interval, which satisfy |f_n(x)| ≤ M_nfor real numbers M_n and all x in the interval. If the series M_n is convergent, prove that the partial sums of the series 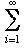f_n(x) are uniformly convergent to a continuous function.
   [Hint: Show that the sequence of partial sums of 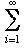f_n(x) are a Cauchy sequence in C[0,1] and then use the result about completeness of this space.]
   This result is known as the Weierstrass M-test after the German mathematician Karl Weierstrass (1815 to 1897).
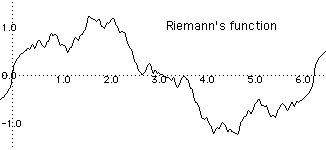
   In 1861 the German mathematician Bernhard Riemann (1826 to 1866) studied the function given by the series 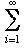sin(n²x)/n² and tried to show that it was a continuous function whose derivative did not exist at any point. Use the last result to prove that this series does define a continuous function.
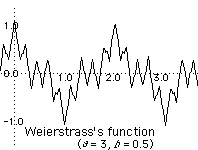
   In fact this function is differentiable, though only at a countable subset of points. In 1872 Weierstrass defined the function 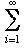bⁿcos(aⁿx) where 0 < b < 1 and a is an odd positive integer with ab > 1. He was able to prove that it is differentiable nowhere. Use the Weierstrass M-test to prove that it is continuous. This was the first such function to be discovered.

        

   Solution to question 2

3. Define a function on the set of integers Z by d(m, n) = 1/2^r if m ≠ n where 2^r is the largest power of 2 dividing m - n and d(m,m) = 0.
   Prove that d is a metric on Z. This is called the 2-adic metric.
   Prove that the sequence (1, 2, 4, 8, 16, ...) converges to 0 in this metric.
   The mathematician Kurt Hensel (1861 - 1941, born in what was Königsberg in Germany and is now Kaliningrad in Russia) used ideas like this to prove results in Number Theory.

   Solution to question 3