Exercises 8

1. If P and Q are any two points in R², prove that d₁(P, Q) ≥ d₂(P, Q) ≥ d_∞(P, Q).
   Hence prove that if a sequence (a₁, a₂, ...) in R² is convergent in the metric d₁ then it is also convergent in d₂ and d_∞.
   Prove also that d₁(P, Q) ≤ √2 d₂(P, Q) and d₂(P, Q) ≤ √2 d_∞(P, Q).
   Deduce that if a sequence (a₁, a₂, ...) in R² is convergent in one of the metrics d₁, d₂, d_∞ then it is convergent in all of them.

   Solution to question 1
   
   

2. Define the function f_n(x) = nxⁿ(1 - x).
   

   
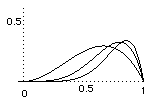
   The graphs of f_n for n = 2, 4, 6 are shown on the right.
   
   

   Prove that the sequence (f_n) converges to the 0-function in the metric d₁ on the space C[0, 1] of continuous functions on [0, 1].
   Use the usual method for finding the turning point of a differentiable function to find the maximum value of f_n on the interval [0, 1].
   What is the limit of this maximum value as n→ ∞? (Use Exercises 6, question 7.)
   Deduce that (f_n) does not converge to the 0-function in the norm d_∞.
   
   

   Solution to question 2

3. Which of the following real-valued functions on the open interval (0, 1) are continuous?

   a) Define a function f on a real-number x by taking the decimal expansion of x (terminating in infinitely many 0's rather than infinitely many 9's if it is an exact decimal) and discarding the first, third, fifth and so on, decimal places.
   So, for example, f ( 0.1234) = 0.24, f (0.1415926536...) = 0.45256... .

   b) Define a function g on a real-number x by taking the decimal expansion of x and replacing 0's by 1's, replacing 1's by 2's and so on except that 9's are replaced by 0's.
   So, for example, g(0.1298) = 0.23091111... (since the infinitely many 0's at the end all get replaced), g(0.1415926536...) = 0.1526037647... .

   c) Define a function h on a real-number x by taking the decimal expansion of x and replacing 0's by 9's, replacing 1's by 8's , 2's by 7's, 3's by 6's, 4's by 5's and vice-versa.
   So, for example, h(0.1298) = 0.9701999999... = 0.9702 (since the infinitely many 0's at the end all get replaced), h(0.1415926536...) = 0.9594073463... .

   [Hint: Observe that the sequence (0.49, 0.499, 0.4999, ...) converges to 0.5 and use the sequential definition of convergence.]

   Solution to question 3