Exercises 7

1. The Heaviside function (named after the English mathematician Oliver Heaviside (1850 to 1925) who also has the ionic layer mentioned in the lyrics of the musical Cats called after him) is defined by:
   h(x) = 0 for x ≤ 0 and h(x) = 1 for x > 0.
   Prove that h is not continuous at 0 using:
   (i) the sequential definition of continuity,
   (ii) the ε-δ definition of continuity.

   Solution to question 1

2. Use the ε-δ definition of continuity to prove that the function f (x) = x² is continuous at the point x = 1.

   Solution to question 2

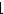3. The function the floor of x is defined to be x rounded down to an integer and is written x.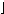
   So for example the floor of 2.6 is 2 and the floor of -3.3 is -4 while the floor of 5 is 5.
   Prove that this function is discontinuous at every integer and continuous elsewhere.
   (You can probably guess what the ceiling of x is.)
   The integer part function is denoted by [x]. So for example [-3.5] = -3 and [2.8] = 2.
   Prove that this function is continuous at 0 but discontinuous at all other integers.
   The fractional part of x is denoted by {x}. Where is this function continuous?

   Solution to question 3

4. Let f and g be functions which are continuous on the whole of R and with f (0) = g (0).
   Prove that the function defined by h(x) = f (x) for x ≤ 0 and h(x) = g(x) for x > 0 is continuous everywhere.
   Hence prove that the absolute value function | x | is continuous everywhere.
   If f is a continuous function on R, prove that the function | f (x) | is also continuous on R.
   If f and g are continuous functions prove that the function M(x) = max{f (x), g (x)} is also continuous.
   [Hint: Prove that max(a, b) =((a + b) + |a - b|)/2 for any real numbers a and b.]
   Prove that the function m(x) = min{f (x), g (x)} is continuous if f and g are.

   Solution to question 4

   
   

5. Use this picture of the unit circle with the angle ABC = x and angle ABD = y to prove that | sin x - sin y | ≤ | x - y |
   Hence prove that the function f (x) = sin x is continuous everywhere.
   Prove that the function cos x is continuous everywhere and hence locate the points where the function tan x is continuous and prove it.
   
   

   Solution to question 5