Exercises 6

1. For each of the following sequences, decide whether they are eventually monotonic (and prove it).
   (a) ( (n+1)/(n+2) )
   (b) (n + 8/n)
   (c) (n + (-1)ⁿ)
   (d) (2n + (-1)ⁿ)

   Solution to question 1

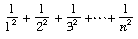2. Let s_n be the partial sum of the series 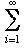(1/i²). Prove that the sequence (s_n) is monotonic and use induction to show that s_n≤ 2 - ¹/_n. Hence prove that the series converges.
   Leonhard Euler (1707 to 1783) showed that its limit is π²/₆.

   Solution to question 2

3. Define a sequence (a_n) by a₁= 1 and a_n+1= a_n+ ¹/_n for n ≥ 1. Prove that the limit as n→ ∞ of |a_n- a_n+1| is 0 but that (a_n) is not a Cauchy sequence.

   Solution to question 3

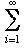4. Let (s_n) be the sequence of partial sums of the positive series b_n. If 0 ≤ b_n≤ c_n and 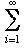c_n has a convergent sequence of partial sums, deduce that (s_n) is monotonic and bounded above and hence convergent.
   This is the so called Comparison Test for positive series discovered by Jacob Bernoulli (1654 to 1705).

   Solution to question 4

5. Let 0 < r < 1 and let (a_n) be a sequence for which |a_n- a_n+1| < rⁿ for all n. Prove that (a_n) is a Cauchy sequence.
   Define a sequence (a_n) by a₁= 0, a₂= 1 and a_n+1= a_n/3 + 2a_n-1/3 for n > 1. Use the last result to show that this is a Cauchy sequence and hence prove that it is convergent.
   Any guesses about what it converges to?

   Solution to question 5

6. For any x > 0 we have x⁰= 1 and 0^x= 0. So is the limit as x→ 0+ of x^x= 0 or 1 or neither?
   What is the limit as n→ ∞ of n^1/n?

   Solution to question 6

7. If you invest £N at a rate of (say)12% per annum simple interest, then at the end of the year you would have £N(1 + 0.12).
   If the interest were calculated twice (i.e. the rate is 6% per 6 months) you would have £N(1 + 0.06)² at the end of the year. (This is called compound interest.)
   If the interest were calculated 3 times a year, you would have £N(1 + 0.04)³ at the end. And so on.
   Compounding more and more often, the number of pounds you would have at the end of the year would be the limit as n→ ∞ of the sequence (a_n) with a_n= N(1+0.12/n)ⁿ.
   Take logarithms, replace 1/n by x and use l'Hôpital's rule to find the limit as x→ 0.

   Solution to question 7