Lattices

This is the study of discrete subgroups of I(Rⁿ). We shall mainly look at the case n = 2.
Our aim is to classify the two-dimensional crystallographic groups in much the same way as we classified the Frieze groups.

In the case of the frieze groups, we took a "smallest translation" and looked at what happened when we applied this to a point. (This is called the orbit of the point.) This gave us a subset of R which we might as well take to be the additive subgroup Z.
We now do something rather similar in R².

Definition
A lattice L is a discrete subgroup of the group Rⁿ (under addition).

Remarks

1. We will usually assume that L does not lie in a lower-dimensional subspace of Rⁿ.

2. Recall that discrete means that there is a minimum distance between points of L.

3. We will usually think of L as a subgroup of the group of translations in I(Rⁿ).
   

Alternative definition
A lattice L is the set {a₁e₁ + a₂e₂ + ... + a_ne_n | a_i ∈ Z } where {e₁ , ... , e_n } is a basis of the vector space Rⁿ.

Remark
Note that the basis constructed above is not the only possible basis.

Examples

1. In R the only lattice is essentially Z.

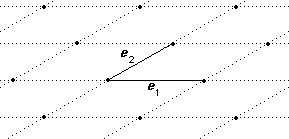2. A general lattice in R²
   For this lattice we choose e₁ and e₂ with no special connections between the lengths or angles of the vectors.
   
   
   
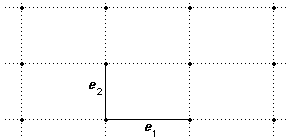3. A rectangular lattice in R²
   We may choose a basis in which e₁ and e₂ are perpendicular
   
   
   
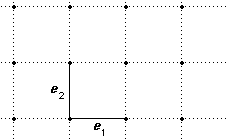4. A square lattice in R²
   A rectangular lattice in which ‖e₁‖ = ‖e₂‖
   
   
   
5. A rhomboidal or isosceles or centred lattice in R²
   
        

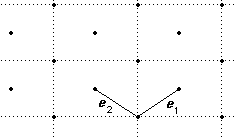
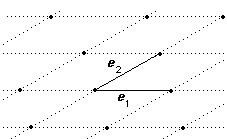
   We have ‖e₁‖ = ‖e₂‖ but e₁ and e₂ are not necessarily perpendicular
   
   
   

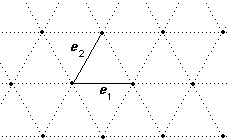6. A hexagonal or equilateral lattice in R²
   A lattice in which ‖e₁‖ = ‖e₂‖ and the angle beween e₁ and e₂ is π/3.
   
   
   
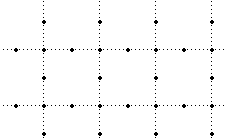7. A non-lattice in R²
   
   
   
8. A simple cubic lattice in R³

9. A body centred cubic lattice in R³

10. A face centred cubic lattice in R³