The crystallographic restriction

We now look at which groups can be the symmetry groups of lattices.

Note that if L is the lattice of translations of a symmetry group G then L is a normal subgroup of G and the quotient group G/L acts on L by conjugation.

The main result is:

The Crystallographic restriction
Any rotation in the symmetry group of a lattice can only have order 2, 3, 4, or 6.

Proof
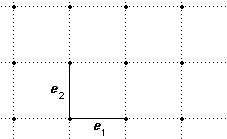
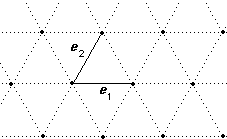
We will give the proof for R². The proof for R³ is similar. It is harder for higher dimensions!
Let L be the lattice and let M be the set of all centres of rotations in S_d(L). This will include L since rotation by π about any lattice point is in S_d, but will in fact be bigger. It will, however, still be discrete.
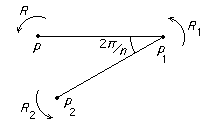Now let p ∈ M be the centre of a rotation R by 2π/n.
Let p₁ ∈ M be a closest point of M which is the centre of a rotation R₁ by 2π/n.
Let p₂ = R₁(p).
Now if T is any transformation mapping a point x to T(x) then conjugating a rotation about x by T gives a rotation (by the same angle) about T(x).
Thus conjugating R by R₁ gives a rotation R₂ by 2π/n about the point p₂ and the diagram shows that if n > 6 the point p₂ would be closer to p than p₁ contradicting the definition of p₁ .


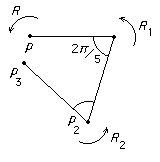A similar proof using this diagram:
with p₃ = R₂(p₁), rules out the possibility that n = 5.




Remark

Note that the cases n = 2 , 3 , 4 and 6 are all possible.
A general lattice can have half-turns as symmetries, a square lattice can be left fixed by rotations by 2π/4 while an equilateral lattice can have rotations by 2π/3 or 2π/6 as symmetries.