Course MT3818 Topics in Geometry
The point groups
Every element in the symmetry group G of Rn is of the form Ta ∘ R with R ∈ O(n). If one composes two such elements, Ta ∘ R1 and Tb ∘ R2 then one gets an element whose linear part is the composite R1 ∘ R2 .
This is the motivation for the following:
Definition
The set of all linear parts of elements of a symmetry group G is called the point group P of G.
Remarks
- The above remark shows that this is indeed a group.
- It often seems that the point group associated with the symmetry group of a pattern is the group of symmetries of the motif and that the point group is then a subgroup of the group of symmetries.
Alas, this is not always true.
Examples
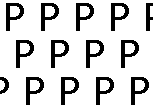 General lattice
General lattice
For this pattern, the symmetry group consists only of translations. That is G = L and so the point group is {I}.
[This is ≅ the symmetry group of the motif ≅ the subgroup fixing a point of the lattice.]
 Rectangular lattice
Rectangular lattice
For this pattern, the symmetry group consists only of translations and compositions Ta∘ V with V a vertical reflection through a lattice point. Hence the point group is generated by V and is D1
[Again this is ≅ the symmetry group of the motif ≅ the subgroup fixing a point of the lattice.]
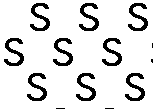 Rhomboid lattice
Rhomboid lattice
The symmetry group consists of translations and compositions Ta∘ H with H a half turn. Hence the point group is generated by H and is C2
[Again this is ≅ the symmetry group of the motif ≅ the subgroup fixing a point of the lattice.]
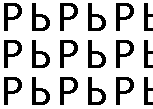 Rectangular lattice
Rectangular lattice
The symmetry group includes a glide reflection which is of the form Ta ∘ R with R a horizontal reflection. Hence the point group is generated by R and is D1
In this case the symmetry group of the motif and the subgroup fixing a point of the lattice are both trivial and so are not the same as the point group. The point group is not a subgroup of the symmetry group.
In fact in general, the point group of G is a factor group of G
Theorem
The point group of a symmetry group G is the factor group G/L where L is the normal subgroup of translations in G.
Proof
Given a symmetry f, we may write it as Ta∘ R with R ∈ O(n) and we may define a homomorphism θ : G 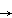 O(n) by Ta∘ R ↦ R
O(n) by Ta∘ R ↦ R
It is easy to verify that this is a group homomorphism with kernel the lattice L of translations and image the point group. The result then follows from the first isomorphism theorem.

Although the elements of the point group P are not elements of the symmetry group G, they do act on the lattice.
Theorem
If A ∈ P ⊆ O(2) and a ∈ L then A(a) ∈ L also.
Proof
Since A is in the point group for some f ∈ G we have f = Tv ∘ A.
Then A ∘ Ta(x) = A(a + x) = A(a) + A(x) = TA(a) ∘ A(x).
Now calculate f ∘ Ta ∘ f -1 which is an element of G.
This is Tv ATa A -1T-v = Tv(TA(a)A)A -1T-v = TvTA(a)T-v = TA(a) and so A(a) is in the lattice.

This means that (notwithstanding the fact that P is not a subgroup of G) that the elements of P act on the lattice and so satisfy the crystallographic restriction. This limits the possible subgroups of O(2) which P can be.
Here are the possible choices for the groups P and the lattices on which they can act. We will see later how the final two columns can be filled in.
| Point group | Lattice | #groups | Names of groups
|
| C1 | general | 1 | p1
|
| C2 | general | 1 | p2
|
| C3 | equilateral | 1 | p3
|
| C4 | square | 1 | p4
|
| C6 | equilateral | 1 | p6
|
| D1 | rectangular
rhomboid | 2
1 | pm pg
cm
|
| D2 | rectangular
rhomboid | 3
1 | pmm pgg pmg
cmm
|
| D3 | equilateral | 2 | p3m1 p31m
|
| D4 | square | 2 | p4m p4g
|
| D6 | equilateral | 1 | p6m
|
JOC February 2003
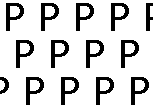 General lattice
General lattice Rectangular lattice
Rectangular lattice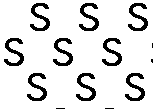 Rhomboid lattice
Rhomboid lattice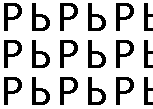 Rectangular lattice
Rectangular lattice O(n) by Ta∘ R ↦ R
O(n) by Ta∘ R ↦ R