Shift vectors

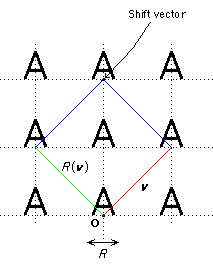
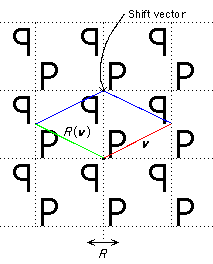
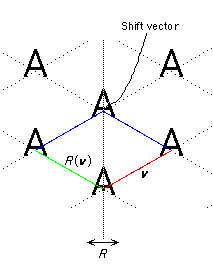
To complete the data we need for classifying the groups, we need one more concept to add to the lattice L, the point group P, and the action of P on L. This is to allow for the fact that some reflections in P act as glides rather than as reflections in G.

Definition

Let A ∈ P be a reflection with T_v ∘ A ∈ G. Then the vector a = v + A(v) is called a shift vector of A.

Properties

1. A shift vector lies in the lattice L.

   Proof
   (T_v ∘ A)²(x) = T_v ∘ A(v + A(x)) = T_v(A(v) + x) since A²= I and this is T_v+A(v)(x) and so v + A(v) is in the lattice.
   
   
   

2. A shift vector of A is left fixed by A.

   Proof
   A(a) = A(v + A(v)) = A(v) + A²(v) = A(v) + v since A² = I and this is a again.
   
   

One can in fact define a shift vector for any element of P.
For example, if R is rotation by 2π/n and T_v ∘ R ∈ G then take a = v + R(v) + R²(v) + ... + R^n-1(v). However, since a is fixed by R it must be 0 and so is not very interesting!

Examples

1. Consider the group of symmetries of this pattern (pm).
   The lattice is rectangular.
   The point group is D₁ which acts on the lattice as vertical reflection R.
   In this case since R is a symmetry, 0 is a shift vector.
   To get another shift vector, take v as shown so that T_v is in the group (and v is in the lattice) and take a = v + R(v) as shown.
   Note that a is on the mirror and so is left fixed by R.
   In this case, if w is a vertical basis element of the lattice, any shift vector of R is of the form 2nw where n ∈ Z.
   
   
   
2. The group of symmetries of this pattern (pg).
   The lattice is again rectangular.
   The point group is D₁ which acts on the lattice as vertical reflection R.
   In this case R is not a symmetry of the pattern.
   To get another shift vector, take v as shown so that T_v is in the group (and v is in the lattice) and take a = v + R(v) as shown.
   As before a is on the mirror and so is left fixed by R.
   Then, if w is a vertical basis element of the lattice, any shift vector of R is of the form (2n+1)w where n ∈ Z.
   
   
   
3. The group of symmetries of this pattern (cm).
   This time lattice is rhomboid.
   The point group is still D₁ and still acts on the lattice as vertical reflection R.
   The vector 0 is a shift vector of R.
   As before, take v as shown so that T_v is in the group (and v is in the lattice) and take a = v + R(v) as shown.
   As before a is on the mirror and so is left fixed by R.
   Then, if w is a vertical basis element of the lattice, then shift vector of R is of the form nw where n ∈ Z. In this case all the lattice points on the mirror are shift vectors.