III: Other point groups

There are nine equivalence classes corresponding to the cases where the point group is D₂ (4 of them), D₃ (2 of them), D₄ (2 of them) and D₆ (one only).

Proof
In all these cases the point group is generated two reflections R₁ and R₂ in lines l and m whose product R₁∘ R₂ is a rotation generating the cyclic subgroup C_n of D_n. So the lines l and m are at an angle of 2π/n and the reflections R₁ and R₂ have shift vectors a = v + R₁v on l and b = w + R₂w on m.
We will find that there are 9 possible combinations of point groups and shift vectors.

Let R, s be the shortest vectors in L on l and m respectively.

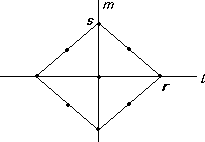
1. If n = 2 (so that l and m are perpendicular) then we can argue as in Stage 2 above:

   If ¹/₂ R + ¹/₂ s ∈ L then both R₁ and R₂ give the cm situation (i) above and we get the group cmm.

   If R and s form a basis for the lattice L then we get three possibilities.
   

   1. The shift vectors of R₁ and R₂ are both 0 and we get the group pmm
      
   2. The shift vectors of R₁ and R₂ are both non-0 and we get the group pgg
      
   3. The shift vectors of R₁ is 0 and that of R₂ is non-0 and we get the group pmg
      
   
   
   
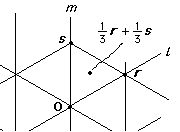2. If n = 3 then the axes of reflection l and m are at 120° or 2π/3.
   Choose R and s as shown.
   In this case all the shift vectors will be 0.
   We get one of the following cases
   
   1. The point ¹/₃ R + ¹/₃ s ∈ L
      In this case, the some of the centres of 3-fold rotation are not on reflective axes.
      The group is called p31m
      
   2. The vectors R and s are a basis for the lattice.
      In this case, the some of the centres of 3-fold rotation are all on reflective axes.
      The group is called p3m1
      
   
   
3. If n = 4 then R and s chosen as above will always be a basis for L and we get two cases.
   
   1. Both shift vectors are 0 ⇒ group is p4m (it should really be called p4mm)
      
   2. One shift vector is 0 and one is not ⇒ group is p4g (it should really be called p4mg)
      
   
   
4. If n = 4 then R and s will be a basis for L and all shift vectors are 0 giving one possibility: the group called p6m.