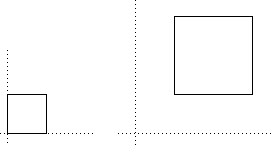
 (x, y) ↦ (1 + 2x, 1 + 2y)
(x, y) ↦ (1 + 2x, 1 + 2y) (x, y) ↦ (1 + x + y, 2 + y)
(x, y) ↦ (1 + x + y, 2 + y)| Previous page (Full finite symmetry groups in 3 dimensions) | Contents | Next page (Affine theorems) |
Recall from an earlier section that a Geometry consists of a set S (usually Rn for us) together with a group G of transformations acting on S.
We now examine some natural groups which are bigger than the Euclidean group. Although the geometry we get is not Euclidean, they are not called non-Euclidean since this term is reserved for something else.
Definition
An affine transformation or affinity of Rn is one of the form Ta ∘ L with Ta a translation and L ∈ GL(n, R).
The group of all such transformations is called the Affine group and is written A(Rn).
Examples
 (x, y) ↦ (1 + 2x, 1 + 2y)
(x, y) ↦ (1 + 2x, 1 + 2y) (x, y) ↦ (1 + x + y, 2 + y)
(x, y) ↦ (1 + x + y, 2 + y)
They do preserve some geometric properties.
If A, B and C are collinear, so are their images under any affine map.
More generally, we have:
Definition
A translation of a linear subspace of Rn is called an affine subspace.
For example, any line or plane in R3 is an affine subspace.
Theorem
Affine transformations map affine subspaces to affine subspaces.
Proof
This follows from the fact that linear maps map linear subspaces to linear subspaces.
Theorem
Parallel lines are mapped to parallel lines.
Proof
Two parallel lines are lines in an affine plane which do not meet. Since affine transformations preserve planes and incidence, their images lie in an affine plane and do not meet. Hence they are parallel.
Theorem
Ratios of lengths of intervals on any line are preserved.
Proof
This follows because such ratios are preserved by linear maps and by translations. 
In fact ratios of lengths on pairs of parallel lines are preserved.
The property of intermediacy (one point being between two others on a line) is also preserved.
| Previous page (Full finite symmetry groups in 3 dimensions) | Contents | Next page (Affine theorems) |