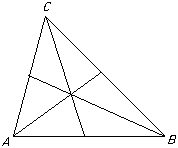
 The medians of a triangle are coincident.
The medians of a triangle are coincident.
Proof
If the triangle has vertices a, b and C then it is easy to verify that the medians meet at the point (a + b + C) /3

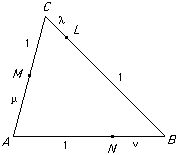 Ceva's theorem (due to Giovanni Ceva in about 1678)
Ceva's theorem (due to Giovanni Ceva in about 1678)If the sides BC, CA, AB of a triangle are divided by points L, M, N in the ratios 1 : λ, 1 : μ, 1 :
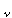 then the three lines AL, BM, CN are concurrent if and only if the product λμ
then the three lines AL, BM, CN are concurrent if and only if the product λμ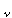 = 1.
= 1.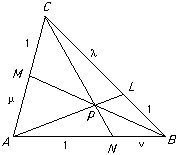 Proof
ProofIn fact, we'll prove this using non-affine methods.
λ = CL/LB = Δ CLA/Δ LBA = Δ CLP/Δ LBP = Δ CAP/Δ ABP.
Similarly μ = AM/MC = Δ ABP/Δ BCP and
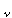 = BN/NA = Δ BCP/Δ CAP and the result follows.
= BN/NA = Δ BCP/Δ CAP and the result follows.
 Menelaus's theorem (due to Menelaus in about 100 AD)
Menelaus's theorem (due to Menelaus in about 100 AD)
If the sides of a triangle are divided by points L, M, N in the ratios 1 : λ, 1 : μ, 1 :  then the three points L, M, N are collinear if and only if the product λμ
then the three points L, M, N are collinear if and only if the product λμ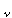 = -1.
= -1.
 Proof
Proof
Note that the ratio in which a point L divides an interval AB is negative if L does not lie inside AB.
Draw AP parallel to ML. Then 1/μ = CM/MA = CL/LP and 1/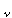 = AN/NB = PL/LB.
= AN/NB = PL/LB.
Then 1/(μ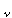 ) = CL/LP . PL/LB = -CL/LB = -λ and the result follows.
) = CL/LP . PL/LB = -CL/LB = -λ and the result follows.
