Similarity geometry

Similarity geometry lies between Euclidean geometry (with group I(Rⁿ)) and Affine geometry (group A(Rⁿ)).

Definition

A similarity transformation or similitude is an affine map which preserves angles.

Theorem
A similarity transformation can be written T_a ∘ λL with L ∈ O(n) and λ > 0.

Proof
Since f is an affine transformation it can be written as T_a ∘ L with L linear. Since f preserves angles, so does L and such a map must stretch all vectors by the same amount and must be a non-zero scalar multiple of an orthogonal transformation.

Any two figures related by a similarity transformation are called similar.
For example, any two squares are similar; any two circles are similar; two triangles are similar if their corresponding angles are equal.

Many of the theorems of so-called Euclidean geometry are in fact theorems of Similarity geometry.
For example, the well-known theorem of Pythagoras can be proved by "similar triangle" methods

Pythagoras's theorem
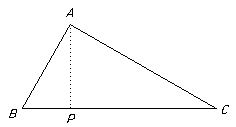
If a triangle ABC has a right angle at A then AB² + AC² = BC²

Proof
Drop a perpendicular to P as shown.
Then the triangles ABC, PBA and PAC are similar and so have their sides in proportion.
Hence AB/PB = BC/BA and AC/PC = BC/AC and so AB² = BP.BC and AC² = BC.PC
Thus AB² + AC² = (BP + PC).BC = BC²