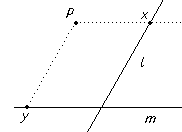Projective spaces

We now set up a geometry based on a space different from Rⁿ.

Early Renaisance artists studied ideas of perspective. That is the problems of representing a three dimensional figure in a convincing way in two dimensions. These artists included Piero della Francesca (1412 to 1492) De prospectiva pingendi, Leone Alberti (1404 to 1472) Della pictura, Leonardo da Vinci (1452 to 1519) etc. Indeed the Greek Anaxagoras of Clazomenae (499BC to 428BC) may have written about perspective.

These ideas were developed into the notion of projective geometry which was studied in the 17th century by (among other) Girard Desargues (1591 to 1661).

We start with the correspondence between points on two lines given by projection from a point P not on either line.

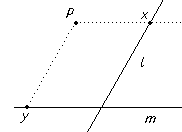Unfortunately, this is not one-one. A line from P parallel to the line m does not meet m and so no point on m corresponds to the point x on l. Similarly no point on l corresponds to the point y on m.

To remedy this we add a point at infinity to each line. Then x ↦ ∞_m and y ↦ ∞_l .
The space we get in this way consisting of the ordinary affine line R and this extra point is called the Real projective line and is written RP¹.


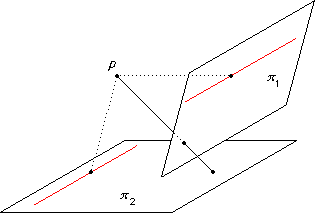Similarly we set up a correspondence between the points of two planes π₁ and π₂ .
This time we add a line at infinity to each plane to make the correspondence into a bijection.
This gives us a space consisting of the ordinary affine plane R² together with this extra (projective) line at infinity which is called the Real projective plane and is written RP².


Remarks

1. Note that we add a single point at infinity to make a projective line. Thus a projective line is really rather like circle and when we add a line at infinity to the plane this is more like a circle at infinity.
   In dealing with infinity on an ordinary real line we think of there being two points at infinity: +∞ and -∞ since we can extend the line in two directions.

   

2. An ordinary line in the plane meets the line at infinity in its point at infinity. A pair of parallel lines meet at their (common) point at infinity. To see this, project so that the line at infinity becomes an ordinary line.
   
   
   
3. Figures related by projection are called projectively equivalent. For example, by thinking of a circular cone as corresponding to projection from the apex of the cone, one can see that any conic section (a parabola, ellipse or hyperbola) is projectively equivalent to a circle and hence any two conic sections are projectively equivalent.
   

4. One can add a single point at infinity to the complex plane and obtain what is called the Riemann sphere. This is then called (rather confusingly) the Complex projective line (since it has dimension 1 over C).