Topology of projective spaces

We may use the representation of projective space via homogeneous coordinates to get a topological picture of these spaces.

1. When we write RP¹ = R² - {(0, 0)}/~ with ~ as before, the equivalence classes are lines through the origin in R².
   Each line meets the "upper semicircle" in a unique point except for the horizontal line which meets it twice.
   Thus RP¹ is the space we get from the semi-circle by identifying its end points. This is a circle S¹.

   One can see the same thing by mapping the line to the circle by stereoscopic projection from the top point of the circle.

2. The space RP² is the set of lines through the origin in R³ - 0. Each line meets the "upper hemisphere" in a unique point except for any horizontal line which meets it twice in opposite points on the equator. Thus can be made out of a hemisphere (topologically equivalent to a 2-dimensional disc) by identifying opposite points on the boundary.
   This can be represented by one of the pictures:

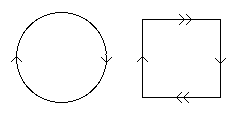
   Alternatively, each line in through the origin in R³ - 0 meets the unit sphere S² in a pair of antipodal points.
   Thus RP² is the space we get from the sphere by identifying antipodal points.

   As a topological space, RP² is non-orientable.