The projective space of a vector space

Given any vector space V over a field F, we can form its associated projective space P(V) by using the construction above.
P(V) = V - {0}/~ where ~ is the equivalence relation u ~ v if u = λv for u, v ∈ V - {0} and λ ∈ F.

Examples

1. With this definition RP¹= P(R²) and RP²= P(R³) so one needs to be careful about dimensions.

2. Let V be vector space C² over the complex numbers C. Then P(C²) is the complex projective line CP¹ which (arguing as in the real case) consists of C together with a single point at infinity.
   Topologically, this is the Riemann sphere S².

3. Let V be a vector space over a finite field F. Such a finite field has p^k elements where p is a prime number. Then if V has dimension n over F, we have |V - {0}| = p^kn - 1 and since each line through 0 in this has p^k - 1 elements on it we get |P(V)| = (p^kn - 1)/(p^k - 1).
   1. For any finite field, with n = 2 we get a projective line with |F| + 1 points consisting of F together with one extra point.
      
      
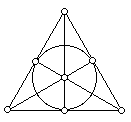
   2. If |F| = 2 and n = 3 we get a projective plane with 7 points.
      The points lie in 3's on 7 lines and each point is the intersection of 3 lines.
      Every pair of points determines a line and every pair of lines meet in a unique point.
      (One of the lines is represented by a circle on the picture.)
      
      
      
   3. If |F| = 3 and n = 3 we get a projective plane with 13 points.
      The points lie in 4's on 13 lines and each point is the intersection of 4 lines.
      Once again every pair of points determines a line and every pair of lines meet in a unique point.

   
   Examples like these last two are very interesting combinatorial objects and have many nice properties.