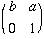Isometries of the line

The group I(R) of isometries of the line R is an interesting and (for such an apparently easy case) complicated group.

Since the group O(1) = {±1} we can divide the elements of the group into two subsets: those with orthogonal part +1 and those with the orthogonal part -1. The former are just translations of the form x ↦ a + x while the latter are maps of the form x ↦ a - x.

These latter maps have the effect of "reversing the direction" on the line. To see more clearly what they do, observe that the point -a/2 is mapped to itself and so you can think of these maps as reflection in this fixed point.
Reflection in the point b is the map x ↦ 2b - x.

Observe that composing two of these reflections gives a translation. Calculation should show you that composing reflections in points b and c gives translation by twice the distace between b and c. The direction of the translation depends on the order in which you do the reflections and so the group is non-abelian.

Notice that translation by any a ≠ 0 has infinite order, while all the reflections have order 2.

We can think about this group I(R) in another way. Since the linear part L ∈ O(1) = {±1} we can represent the element T_a∘ L by the pair (a, ±1).

This gives I(R) = {(a, b) ∈ R² | b = ±1 } and composing the maps gives a multiplication * on these pairs defined by

(a₁ , b₁)*(a₂ , b₂) = (a₁ + b₁a₂ , b₁b₂).

It is now no longer obvious that the multiplication is associative. The identity element (which is, of course, the pair representing the map x ↦ x) is the pair (0,1). The inverse of an element (a, 1) is (-a, 1) (translation in the opposite direction) while an element (a, -1) is its own inverse.

The group of matrices { 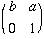| a, b ∈ R, b = ±1 } is isomorphic to I(R). See Exercises 3 Question 3.