Isometries of the plane

Many of the observations made about the group of the line can also be applied to I(R²): the isometries of the plane R².

Again we can divide the isometries into two subsets: those for which the orthogonal transformation is in SO(2) (with determinant +1) and those with determinant -1. These are called direct and opposite symmetries respectively.

1. Direct symmetries

   Here is a complete classification of direct symmetries.

   Theorem
   Any direct symmetry is either a translation or rotation about some point.

   Proof
   

   1. If f has a fixed point b then T_-b∘ f ∘ T_b(0) = 0 and so this is a length preserving map which fixes the origin and hence is a linear map. Thus it is in SO(2) and is rotation about 0. Hence f is rotation about the point b.

   2. We have f = T_a∘ L with L ∈ SO(2) ⇒ f(x) = a + L(x). Now we try to solve f(x) = x = a + L(x) to find a fixed point. That is, we look for a solution of (L - I)x = -a. The only case in which we could not find such a solution is if L - I were not invertible. That is, if +1 were an eigenvalue of L. But the only element in SO(2) with +1 as an eigenvalue is the identity. Hence if f fails to have a fixed point, L = I and f is a translation.
      
      
      
2. Opposite symmetries

   We now classify the opposite symmetries. There are two kinds.

   Theorem
   An opposite symmetry of R² is either reflection in any line or is a glide reflection.

   Proof
   Note that the reflection may be in a line not necessarily through 0.
   A glide reflection (or glide) is a reflection in a line followed by a translation in a direction parallel to that line.

   Since any element in O(2) - SO(2) is a reflection in a line through 0, the result follows from:

   Lemma
   Let R_b be reflection in a line through 0 containing the vector b. Then T_a ∘ R_b is a reflection if a and b are perpendicular and a glide-reflection otherwise.

   Proof
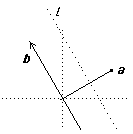   From the diagram, if a and b are perpendicular, then T_a ∘ R_b is reflection in the line l parallel to b through the point a/2.
   
   
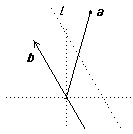   If a and b are not perpendicular, then points of l are mapped to other points of l and so f acts on l by translation. Points on one side of l are mapped to the other side and so we have a glide along l.
   
   
   
   
   

1. Note that glide reflections are really the most general form of an opposite symmetry. A reflection could be considered as a glide where the translation happens to be trivial.

2. Glide reflections have no fixed points and so we get the following summary about isometries of R².

   	Direct	Opposite
   Fixed point	Rotation	Reflection
   No fixed point	Translation	Glide

   
   

3. Products of direct symmetries are direct. It is however, possible for the product of rotations to be a translation.

4. Products of reflections are rotations if the "mirror lines" meet and translations if they are parallel.

5. Any isometry of R² can be written as a product of at most three reflections in lines.