Exercises 9

1. Two triangles A₁B₁C₁ and A₂B₂C₂ in R³ are in perspective from O if A₁A₂ , B₁B₂ and C₁C₂ meet at O. The intersection of the planes A₁B₁C₁ and A₂B₂C₂ is called the axis of perspective.
   Prove that for two such triangles the four axes of perspective of the pairs A₁B₁C₁ , A₂B₂C₂ : A₂B₁C₁ , A₁B₂C₂ : A₁B₂C₁ , A₂B₁C₂ : A₁B₁C₂ , A₂B₂C₁ are coplanar.
   [Project the axis of the pair A₁B₁C₁ , A₂B₂C₂ and the point O to the plane at infinity in RP³ and then look at what this does to the picture.]

   Solution to question 1

2. Show that the elements of PGL(2, R) which map a line to itself form a subgroup isomorphic to the Affine group A(R²).
   Deduce that one may recover Affine Geometry from Projective Geometry by considering only those maps which take the line at infinity to itself.

   Solution to question 2

3. Deduce a result from Pascal's Mystic Hexagram Theorem by making consecutive vertices coincide.
   Use Brianchon's theorem to deduce a property of a triangle which circumscribes a conic. (i.e. the three sides of the triangle are tangents to the conic.)
   In the case when the conic is a circle, give an independent proof of this.

   Solution to question 3

4. Given five points on a conic, use Pascal's theorem to construct any number of other points on the conic.

   Solution to question 4

5. A circle in the elliptic plane is a set { y | d(x, y) = r } for a fixed x ∈ RP² and r > 0.
   By drawing the corresponding curves on the 2-sphere S² find two circles in the elliptic plane which intersect in four points.

   Solution to question 5

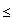6. If an elliptic triangle has angles 0 < α β 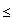γ then prove that β + γ < π + α.
   For which integers p, q, r ≥ 2 is there an elliptic triangle with angles π/p, π/q, π/r ?

   Solution to question 6

7. In what range do the angles of a regular p-gon in the elliptic plane lie?
   Which regular p-gons can be used to tile the elliptic plane?

   Solution to question 7