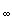Exercises 2

1. Prove that the metrics d₁ , d₂ and d on R² do indeed satisfy the triangle inequality. What about the corresponding metrics on Rⁿ ?

   Solution to question 1

2. Define a metric on the unit circle in R² by d(X, Y) = the length of the arc XY. Hence or otherwise prove that the formula d(x, y) = min{ |x - y|, 1 - |x - y| } defines a metric on the open unit interval (0, 1). Does the same formula define a metric on the closed interval [0, 1] ?

   Solution to question 2

3. Let p be a prime number. Define a function f on the positive integers N by the formula
   f (n) = p^k where this is the largest power of p dividing n and a function g on the rationals Q by g(a/b) = f (|a|) / f (|b|) so that g(r) is the "largest power of p dividing r".
   Prove that the function d given by d(r, s) = 1/g(|r - s|) defines a metric on Q.
   [This is called the p-adic metric.]
   Prove that in this metric the sequence (p, p² , p³ , ... ) converges to 0.

   Solution to question 3

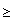4. If P and Q are any two points in R², prove that d₁(P, Q) d₂(P, Q) 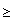d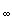(P, Q).
   Hence prove that if a sequence (a₁ , a₂ , ...) in R² is convergent in the metric d₁ then it is also convergent in d₂ and d.
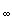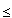
   Prove also that d₁(P, Q) 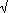2 d₂(P, Q) and d₂(P, Q)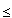 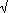2 d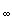(P, Q).
   Deduce that if a sequence (a₁ , a₂ , ...) in R² is convergent in one of the metrics d₁ , d₂ , d 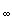then it is convergent in all of them.

   Solution to question 4

5. Which of the following real-valued functions on the open interval (0, 1) are continuous?
   
   
   
   1. Define a function f on a real-number x by taking the decimal expansion of x (terminating in infinitely many 0's rather than infinitely many 9's if it is an exact decimal) and discarding the first, third, fifth and so on, decimal places.
      So, for example, f( 0.1234) = 0.24, f (0.1415926536...) = 0.45256... .

   2. Define a function g on a real-number x by taking the decimal expansion of x and replacing 0's by 1's, replacing 1's by 2's and so on except that 9's are replaced by 0's.
      So, for example, g(0.1298) = 0.23091111... (since the infinitely many 0's at the end all get replaced), g(0.1415926536...) = 0.2526037647... .

   3. Define a function h on a real-number x by taking the decimal expansion of x and replacing 0's by 9's, replacing 1's by 8's , 2's by 7's, 3's by 6's, 4's by 5's and vice-versa.
      So, for example, h(0.1298) = 0.9701999999... = 0.9702 (since the infinitely many 0's at the end all get replaced), h(0.1415926536...) = 0.9594073463... .
      
   
   [Hint: Observe that the sequence (0.49, 0.499, 0.4999, ...) converges to 0.5 and use the fact that continuous functions map convergent sequences to convergent sequences.]

   Solution to question 5