Let X = {x ∈ [a, b] | f (y) ≤ 0 for all y ∈ [a, x]}. Then X is non-empty since a ∈ X and X ⊆ [a, b] so it is bounded. Hence by the Completeness Axiom, X has a least upper bound α (say).
We claim that f (α) = 0.
Proof of that:
We will show that either of the assumptions f (α) > 0 or f (α) < 0 leads to a contradiction and the result then follows from the Trichotomy property of the Order Axiom.
So suppose f (α) > 0. Say f (α) = ε. Then for some δ > 0 we have f (x) > 0 for x lying in the interval (α - δ, α + δ).
But then α - δ would be an upper bound of X, contradicting the fact that α is the least upper bound.
Similarly, suppose f (α) < 0. Say f (α) = -ε. Then for some δ > 0 we have f (x) < 0 for x lying in the interval (α - δ, α + δ).
But this is a contradiction since α is an upper bound of X.
This completes the proof.

- You should compare this to the earlier proof of the existence of √2. The fact that these two proofs are so similar is no coincidence, since we could prove the existence of √2 by applying the intermediate value theorem to the function f (x) = x2 - 2 on the interval [1, 2].
- The reason that this result is called the Intermediate Value Theorem comes from the following corollary.

- Any real polynomial of odd degree has a real root.
Proof
Suppose p(x) = xk+ ak-1xk-1+ ... + a1x + a0. Then as x→ ∞, p(x)→ ∞. Also, since k is odd, as x→ -∞, p(x)→ -∞. Hence one can find an interval on which p changes sign and so we must have a real root.

- Solving an equation f (x) = 0.
- The bisection method
Find an interval [a, b] on which the function changes sign. Then evaluate f at the midpoint (a+b)/2 and choose whichever subinterval f changes sign on. Then repeat to get smaller and smaller subintervals.
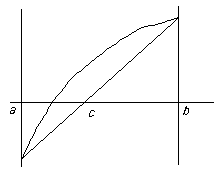
- The method of false position
The same idea, but this time instead of taking the midpoint of the interval, linearly interpolate between (a, f (a)) and (b, f (b)) to decide where to split the interval. In fact, this is at the point c = (b f (a) - a f (b))/(f (a) - f (b)).
These methods are both very robust and do not require assumptions about differentiability needed, for example, for the (usually) faster Newton-Raphson method.
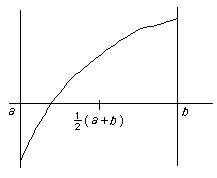
- The bisection method
- The intermediate value theorem can be used to prove a variety of simple "real-life" results.
- The mashed potato theorem
A plate of mashed potato can be evenly divided by a single straight vertical knife cut.Proof
In position K1 less than half the potato is at the left of the knife, in position K2 more than half is at the left. Hence (by the intermediate value theorem) there is an intermediate position where exactly half is at one side.
You may care to think of how continuity should be involved in this argument.

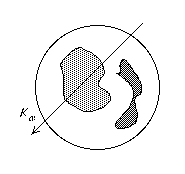
- The mashed potato and beans theorem
A plate of mashed potato and baked beans can be evenly divided by a single straight vertical knife cut.Proof
Choose one particular angle and the last result shows that you can divide the potatoes by a cut Kα at this angle. Then (say) there will be more than half the beans on the left of the cut. Now vary the angle continuously by π (180 degrees) until the knife is in the same position as before, but pointing the other way. At each angle, make sure you bisect the potatoes. Now less than half the beans are on the left and so you passed through an intermediate position where both beans and potatoes were divided fairly.
This result even holds true if you pile the beans on top of the potato (or vice versa).

- Note that the above two results were achieved with vertical cuts. If you allow cuts which are not vertical, you can use the extra "degree of freedom" to prove:
The bowl of fruit theorem
An apple, a pear and a banana can be equally divided by a single knife-cut.Proof
Exercise.

RemarksThis last result is usually called the Ham Sandwich Theorem (two pieces of bread and the ham).
By putting the three pieces of fruit far apart, you should see that you do not have any freedom to deal with a fourth volume. If you move from three dimensions to four, though ...
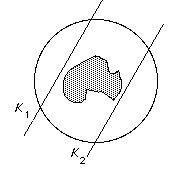
- The mashed potato theorem
| Previous page (The Weierstrass approximation theorem) | Contents | Next page (The boundedness theorem) |